七年级数学暑假作业测试2 姓名 分数
一、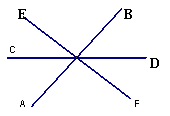
选择题（20分）填在后面的表格中
1.如图：直线AB、CD相交于O点，直线EF⊥AB于O点，
∠COE＝
，则∠BOD＝（ ） ：A. B.
C.
D.
2.如图：平移线段AB到
的位置，再继续平移到
，连接
图中的平行四边形有（ ）个：
A. 2 B. 3 C. 4 D. 5 。
3.若点P
是第一象限内的点，则
满足：A. 
B.
C.
D.
4. 在平面直角坐标系
中，已知
，在
轴上确定点P，使⊿
为等腰三角形，则符合条件的点有：A. 2个 B.3个 C.4个 D. 5个
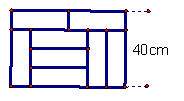
5.如图：用8个相同的长方形地砖拼成一个矩形，则每个长方形
地砖的面积是：A. 200
B 300 C. 
D. 2400
6. 若
，则化简
的结果：A. 0 B. 
C. 
D. 
7. 光线以如图所示的角度
照射到平面镜I上，然
后在平面镜I，II之间来回反射，已知∠
，
∠
，则∠
：A.
B. 
C. 
D.
8. 代数式
，当
时，其值为3；当
时，其值为4，则代数式
的值是：A.
B.
C.
D.
9. 甲从一个鱼摊上买了三条鱼，平均每条
元，又从另一个鱼摊上买了二条鱼，平均每条
元，后来他又以每条
的价格把鱼卖掉，结果发现赔了钱，原因是：A. 
B. 
C. 
D. 与和的大小无关。
10. 下列各组数中，互为相反数的一组是：A. 
B. 
C. 
D. 
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 |
二、填空题（30分）
10. 若点
在第二象限，则
在第 象限。
12. 一个正数
的两个平方根分别是
和
，则
；
。
13. 三角形的三条边的长
均为正整数，且
，当
时，符合上述条件的三角形有 个。
14. 时针指道八点二十分时，时针与分针所成的夹角的度数为 。
15. 用科学计数法表示为 。
16. 已知点
，
，如果
∥轴，且线段的长为5，则
的值为 。
17. 用三块正多边形的木板铺地，拼在一起并使其交于一点的各边完全吻合，若其中两块木板的边数均为5，则第三块木板为正 边形。
18. 在2002年世界杯足球预选赛亚洲“十强”赛中，规定胜一场记3分，平一场记1分，负一场记0分，中国队共赛八场获得19分，其中只输一场，那么中国队胜 场。
19.已知
，则
。
20.若
，则 。
二、解答题（70分）
21.（6分）解不等式组，并将其解集表示在数轴上
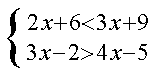
22.（6分）若
，
求
的值
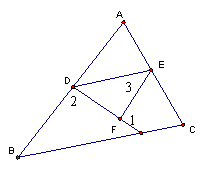
23.（8分）如图，已知∠1＋∠2＝
，∠3＝∠B，试判
断∠AED与∠C的关系，并说明理由。
24. （8分）在直角坐标系中，四边形ABCD各个顶点的坐标为A（-1，3），B（-3，2），C（-4，0），D（0，0），（1）求四边形的面积。
（2）如果把四边形ABCD各个顶点的横坐标加2 ，纵
坐标减1，所得四边形的面积又是多少？
25. （10分）某产品每件成本10元，试销阶段每件产品的销售价x（元）与产品的日销售量y（件）之间的关系如下表：
| x （元） | 15 | 20 | 25 | … |
| y （件） | 25 | 20 | 15 | … |
若日销售量y是销售价x的一次函数．
（1）求出日销售量y（件）与销售价x（元）的函数关系式；
（2）求销售价定为30元时，每日的销售利润．
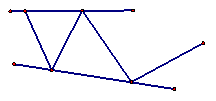
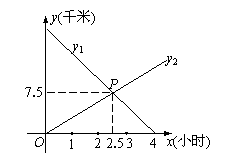26. （10分）小东从A地出发以某一速度向B地走去，同时小明从B地出发以另一速度向A地而行，如图所示，图中的线段
、
分别表示小东、小明离B地的距离（千米）与所用时间（小时）的关系。
⑴试用文字说明：交点P所表示的实际意义。
⑵试求出A、B两地之间的距离。
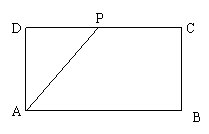27. （10分）如图，在长方形
中，∠
，
，点P从起点D出发，沿DC、CB向终点B匀速运动。设点P所经过的线段长为，点P所经过的线段与线段AD、AP所围成图形的面积为。
（1）求与之间的关系式。
（2）根据图像，求的值最大时，的值为多少？并求出的最大值。
28. （12分）某工厂生产某种产品，每件产品的出厂价为100元,其成本价为50元，因为在生产过程中。平均每生产一件产品有0.5m3的污水排出，所以为了净化环境，工厂设计了两种方案对污水进行处理，并准备实施。（12分）
方案1：工厂污水先净化处理再排出。每处理1m3污水所用原料费为4元，并且每月排污设备损耗费为60000元。
方案2：工厂将污水排到污水厂统一处理，每处理1m3污水需付28元排污费。
（1）设工厂每月生产x件产品，每月利润为y元，分别求出依方案1和方案2处理污水时，y与x的函数关系式
（2）设工厂每月生产量为6000件时，你若作为厂长在不污染环境，又节约资金的前提下应选用哪种处理污水的方案？请你通过计算加以说明。