解一元一次不等式——不等式的变形(一)
主备人:孙立强
一、教学目标:使学生通过自主探究,理解和掌握不等式的基本性质1、2、3,并会用不等式基本性质将不等式变形
二、重点:运用不等式基本性质对不等式进行变形。
难点:不等式基本性质的应用。
三、预习内容:课本第58~60页,以及目标手册第62~64页的“当堂课内练习”。完成下列填空:
1、 不等式性质1:如果a>b,那么____________,____________。即不等式的两边都加上(或减去)_________或__________,不等号的方向______。
2、 完成课本第59页的“试一试”,并填空:
不等式性质2:如果a>b,并且c>0,那么ac____bc. 即:不等式两边都乘以(或除以)同一个_______,不等号方向______。
不等式性质3:如果a>b,并且c<0,那么ac____bc. 即:不等式两边都乘以(或除以)同一个_______,不等号方向_______。
3、 解不等式的过程,就是将不等式变形成__________或_______的形式.并与解方程相比较:
4、 仿照课本第59页例1,第60页例2,完成第60页练习。
5、 完成目标手册第64页的“当堂课内练习”。
四、尝试练习一:
1、 方程2x=8的解有___个,不等式2x<8的解有___个.
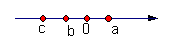
2、 有理数a、b、c在数轴上的位置如图,试用“>”、“=”、“<”填空。
(1)
|
(2) a+b____a+c , a-b____c-b. a-b____a-c.
(3)
![]() _____
_____![]()
3、 当a>0,b_____0时, ab>0 ; 当a<0 ,b___0时,ab<0 。
4、 在数-4,-3,-2,-1,0,1,2,3,4中选出适合下列不等式的数填空:
(1)-5<n:_______________;(2)7a≥13:_____________________
(3)x<(-3)(+4):________________________.
5、 解下列不等式,并在数轴上表示结果:
(1)![]() (2) 7x-4<5+6x
(3)-2x<6
(2) 7x-4<5+6x
(3)-2x<6
(4) –x+3>4 (5) 4x-15>3x-2 (6) 5+6x≥5x
教师讲解内容:
1、 根据学生在预习过程中发现的问题,予以讲解、纠正。
2、 课本第60页两个问题,学生能否解释。
3、 例题:
(1) 如果x>-2,那么x-m_____-2-m。
(2) 如果a<b,那么a+6___b+6,a-2_____b-2。
(3) 如果7m-2b<7n-2b,那么7m___7n,7m+1_____7n+1。
(4) 如果b>0,那么a-b___a;b=0, 那么a-b___a;b<0,那么a-b____a。
(5) 如果a<-b,那么a+b____0.
4、 求下列不等式的解集,并在数轴上表示出来。
(1)x-5>7 ( 2)4x-15>3x-2 (3)5+6x≤3x-1 (4)3x-2x<0
5、 求不等式x-2<4的正整数解,并在数轴上表示出来。
思考题:已知:![]() 。
。
(1) 当y>0时,a为何值?
(2) 当y<0时,a为何值?
教后感:
五、尝试练习二:
1、若a<0,b=-a,则下列各式中成立的是( )
A ![]() <0
B
<0
B ![]() <
<![]() C
C ![]() D
D ![]()
2、如果a<b<0,那么下列各式中正确的是( )
A ![]() >
>![]() B
B ![]() <
<![]() C a<b D
C a<b D ![]() <
<![]()
3、如果8+2a<8+2b,那么a、b的关系是( )
A a=b B a<b C a>b D以上均不对
4、不等式3+x≥6的解集是( )
A x=3 B x≥3 C x>3 D大于或等于3的整数
5、下列说法正确的( )
A 方程4+x=8和不等式4+x>8的解是一样的 B x=2是不等式4x>5的唯一解
C x=2是不等式4x>5的一个解 D 不等式的两边都加上1,则此不等式成立。
六、课堂作业:
(一)选择题:
1、已知a>b>0,c是一个有理数,下列各式正确的是( )
A ![]() >
> ![]() B ac>bc C a-3c<b-3c D 以上均不对
B ac>bc C a-3c<b-3c D 以上均不对
2、x、y都是有理数,下列各式正确的是( )
A
x+y>x-y B xy>![]() C 2x+3y>x+2y D以上均不对
C 2x+3y>x+2y D以上均不对
3、已知x<1,下列各式正确的是( )
A ![]() <1 B
<1 B ![]() >1 C 1-x>0
D x<1
>1 C 1-x>0
D x<1
4、不等式1+a>a-1的解是( )
A x=0 B 无解 C 所有有理数 D 这个不等式无意义
5、满足x<6的非负整数解有( )个。
A 5 B 6 C 7 D 无数个
(二)解下列不等式,并在数轴上表示出解集。
1、x-7≥16 2、 1-3x>0 3、-9x<14 4、-2x>0
5、8x-7≤15
6、1-x>2x
7、![]() <
<![]()
解一元一次不等式——不等式的变形(二)
主备人:孙立强
一、教学目标:进一步理解和掌握不等式的基本性质,并会用不等式基本性质解不等式。
二、重点:运用不等式基本性质解不等式。
难点:不等式基本性质的应用。
三、预习内容:目标手册第65~66页课内练习。
四、尝试练习一:
(一)填空:
1、 已知a>b,则a+c_____b+c,a-c____b-c。
2、 已知a>b,c>0,则ac___bc,![]() _____
_____![]() 。
。
3、 已知a>b,c<0,则ac___bc,![]() _____
_____![]() 。
。
4、 设a<b,用“>”或“<”填空:a+2____b+2; a-5____b-5; -a____-b;
![]() ____
____![]() ;
-2a______-2b; 2a_____a+b
;
-2a______-2b; 2a_____a+b
5、 若a+2>b+2,则a-7____b-7, ![]() ____
____![]() .
.
(二)选择题:
1、若a<b,则下列各式仍然成立的是( )
A ac<bc B ac>bc C a-c<b-c D a(-c)<b(-c)
2、若x<y,则下列各式错误的是( )
A
6x<6y B x+4<y+3 C x-3<y-3 D ![]() >
>![]()
(三)根据不等式的基本性质,把下列各式化为x>a或x<a(a为常数)的形式:
1、x+3<2 2、![]() 3、-3x>6 4、
3、-3x>6 4、![]()
五、尝试探究:
1、 方程2x=-6与-2x=6的解相同,不等式2x>-6与-2x>6的解集相同吗?
2、 已知关于的不等式![]() 的解集是
的解集是![]() ,求
,求![]() 的取值范围。
的取值范围。
3、 由不等式![]() 如何变形成
如何变形成![]() ?你能说出它的变形过程吗?试一试。
?你能说出它的变形过程吗?试一试。
教案
例题:
1、 已知![]() ,求关于x的不等式
,求关于x的不等式![]()
![]() 的解集。
的解集。
2、 已知a<b,讨论ab与a![]() 的大小关系。
的大小关系。
3、 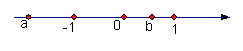 由
由![]() ,可推出(1)
,可推出(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() ;(4)
;(4)![]() 。其中正确的有哪些?说明理由。
。其中正确的有哪些?说明理由。
4、 利用不等式的基本性质求不等式![]() 的正整数解。
的正整数解。
5、
|
教后感:
六、尝试练习二:
1、 若方程![]() 的解为x=-1,那么a、b之间的关系示什么?
的解为x=-1,那么a、b之间的关系示什么?
2、 求出适合下列不等式的x的整数解:
(1) 1<x<6:___________________;(2) -5<x<-1:_______________________
(3) x≤4:____________________;(4) 2≤x≤4:_____________________.
七、课堂作业:
(一)、填空:
1、 当x______时,代数式![]() 的值是正数;当x_______时,代数式
的值是正数;当x_______时,代数式![]() 的值是负数;当x________时,代数式
的值是负数;当x________时,代数式![]() 的值是零.
的值是零.
2、 若a>0,则不等式ax>b的解集为_________;若a<0,则不等式ax>b的解集为__________.
3、 代数式x-2的值 不大于0,则x_______。
4、 已知x<л,则满足条件的非负数x=_________。
(二)选择题:
1、若a、b为有理数,在下列条件下,结果正确的是( )
A 若a<b,则2-a<2-b B 若a>b,则-2a>-2b
C 若a<b,则![]() D 若a>b,则
D 若a>b,则![]()
2、如果![]() ,那么m的值是( )
,那么m的值是( )
A 不小于![]() B 不大于
B 不大于![]() C 大于
C 大于![]() D 等于
D 等于![]()
3、若abcd>0,且a+b+c+d>0,则a、b、c、d中负数最多有( )
A 1个 B 2个 C 3个 D 4个
4、如果-m,1-m, m和m+1四个数在数轴上所对应的点从左到右的顺序排列的话,那么( )
A m>0 B m<0 C m>![]() D m为一切有理数
D m为一切有理数
(三)有一个两位数,个位上的数是a,十位上的数是b,如果把这个两位数的个位与十位上的数对调,得到的两位数大于原来的两位数,那么a与b哪个大?