七年级数学第二学期第一次月考检测卷
一、选择题（本大题共10小题，每题4分，共40分）
1．一元二次方程x2= —3x的解是（ ）
A．0 B．－3 C．0或－3 D．0或3
2．下列分式中一定有意义的是（ ）
A．
B．
C．
D．
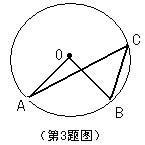
3．如图，C是⊙O是一点，O是圆心，若，则的度数为（ ）
A．
B． 
C．
D．
4．把方程配方正确的是（ ）
A．
=0 B．－2=0 C．
+1=0 D．－2=0
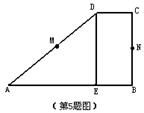
5．如图，设M，N分别是直角梯形ABCD两腰AD，CB的中点，DE
AB于点E，将沿翻折，M与N恰好重合，则AE：BE等于（ ）
A．2：1 B．1：2 C．3：2 D．2：3
6．已知，⊙O
和⊙O
的半径分别是3cm和5cm，如果这两圆没有公共点，则圆心距的范围是（ ）
A．d ＞8 B．0＜d＜2 C．2＜d＜8 D．d＞8 或 0＜d＜2
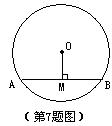7．如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是（ ）
A．4 B．6 C．7 D．8
8．根据下列表格的对应值：
| x | 3.23 | 3.24 | 3.25 | 3.26 |
| ax2+bx+c | －0.06 | -0.02 | 0.03 | 0.09 |
判断方程（为常数）一个解的范围是（ ）
A．3＜x＜3.23 B．3.23＜x＜3.24 C．3.24＜x＜3.25 D．3.25＜x＜3.26
 |  |  | |||
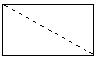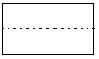9．下列矩形中，按虚线剪开后，既能拼出平等四边形和梯形，又能拼出三角形的是（ ）
A．
B．
C．
D．
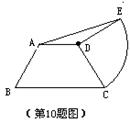
10．已知等腰梯形ABCE中，AD∥BC，AD=3，BC=5，腰CD绕点D逆时针旋转
至DE，连接AE，ADE的面积为（ ）
A．1.5 B．3 C．2 D．
二、
填空题（本大题共6小题，每题5分，共30分）
11．请在下面“ , ”中分别填入适当的代数式，使等式成立。
+
=
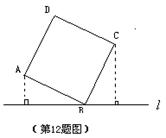12．如图，直线
过正方形ABCD顶点B，点A、C到直线的距离分别是1和2，则正方形的边长为 。
13．书架上有2本相同的数学书和2本相同的语文书，则从中随意取出2本书，恰好是一数学书，一本语文书的概率为 。
14．从一个半径为3的圆形纸片上取圆周的
剪下一个扇形，将它围成一个圆锥的高为
。
15．开口向下的抛物线y=
的对称轴经过点（—1，3），则m=
16．如图是小李发明的填图游戏，游戏规则是：把5，6，7，8四个数分别填入图中的空格内，使网格中每行，每列的数学从左到右和从上到下都按从小到大的顺序排列，那么一共有
| 1 | 2 | |
| 3 | 4 | |
| 9 |
种不同的填法。
三、解答题（本大题共8小题，共80分）
以下各题须写出具体解答过程
17．计算或化简
(1) 计算：
(2) 化简：
18．直角三角形的两条直角边边长是方程
的两个根。求该直角三角形的两直角边以及它的外接圆周长。（本题8分）
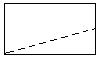
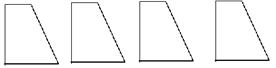
19．请将四个全等直角梯形（如图），拼成一个平行四边形，并画出两种不同的拼法示意图（拼出的两个图形只要不全等就认为是不同的拼法）（本题8分）
20．A城市每立方米的水费是B城市的1.25倍，同样交水费20元，在B城市比在A城市可多用2
水，那么A，B两城市每立方米的水费各是多少？（本题10分）
 |
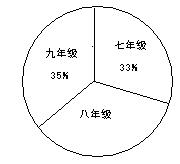
21．在植树节来临之际，腾飞中学抽调200名学生去参加植树活动，下面是根据植树情况绘制的频数分布直方图和参加植树人数比例分布的扇形统计图。由题中提供的信息请解答下列问题：（本题10分）
（1） 八年级学生共植树多少棵？
（2）
 |
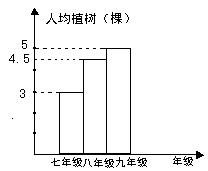参加植树的学生平均每人植树多少棵？
 |
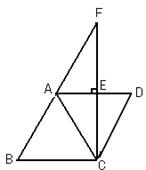
22．如图，直线CF垂直且平分AD于点E，四边形ADCB是菱形，BA的延长线交于CF点F，连接AC。（本题10分）
（1） 图中有几对全等三角形，请把它们都写出来；
（2） 证明：ABC为正三角形。
 |
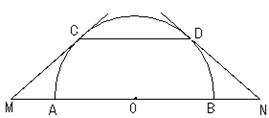
23．已知：如图，AB是半圆O的直径，弧AC与弧BD相等，直线CM、DN分别切半圆于点C、D，且分别和直线AB相交于点M、N。（本题12分）
（1） MO与NO相等吗？为什么？
（2） 若M=30，试探索线段MN与线段CD的关系。
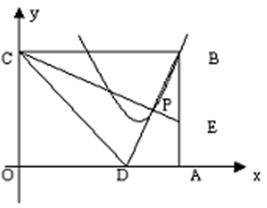
24、（本题14分）一张矩形纸片OABC平放在直角坐标系内，O为原点，点A在X轴的正半轴上，点C在Y轴的正半轴上，OA=5，OC=4。
⑴如图，将纸片沿CE对折，点B落在X轴上的点D处，求点D的坐标；
⑵在⑴中，设BD与CE的交点为P，若点P，B在抛物线y=x2+bx+c上，求b，c的值；
 |
⑶设⑵中的抛物线与BC边的另一个交点为Q，则在该抛物线上以及它的对称轴上是否分别存在点M与点N（点M在抛物线上，点N在它的对称轴上），使得以M，N，B，Q为顶点的四边形为平行四边形。若存在，求出点M 的坐标；若不存在，请说明理由。