第四章 平面图形及其位置关系
一、 本章关键词
点 线(直线 射线 线段 它们的表示方法及性质 线段的比较 线段的中点) 角(两种定义
表示方法 比较方法 角的平分线) 平行线(定义 特征) 垂直(定义 特征 点到直线的距离)
二、 基础训练
1.如图,A,B在直线l上,下列说法错误的是 ( )
![]()
A.线段AB和线段BA同一条线段
B.直线AB和直线BA同一条直线
C.射线AB和射线BA同一条射线
D.图中以点A 为端点的射线有两条。
2. 下列说法正确的是 ( )
A.经过两点有且只有一条线段
B.经过两点有且只有一条直线
C.经过两点有且只有一条射线
D.经过两点有无数条直线
3.在图中,不同的线段的条数式( )
![]()
A.3 B.4 C.5 D.6
4.在一个平面内,经过一个点可以画 条直线;经过两点可以画 条直线;经过三点中的任两点可以画 条直线;经过四点中的任两点可以画直线,最少可以画 条直线、最多可以画 条直线。
5.下列说法正确的是( )
A. 两点之间的连线中,直线最短 B.若P是线段AB的中点,则AP=BP
C. 若AP=BP, 则P是线段AB的中点 D. 两点之间的线段叫做者两点之间的距离 6.如果线段AB=5cm,线段BC=4cm,那么A,C两点之间的距离是( )
A. 9cm B.1cm C.1cm或9cm D.以上答案都不对
7. 如图,AB=8cm,O为线段AB上的任意一点, C为AO的中点,D为OB的中点,你能求出线段CD的长吗?并说明理由。 ![]()
8线段AB=16cm,C是直线AB上的一点,且AC=10cm,D是AC的中点,E是BC的中点, 求线段DE的长.
9.如图,以O为顶点且小于180º的角有( )
A.7个 B.8个 C.9个 D.10个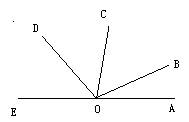
10.36.33º可化为( )
A.36º30´3" B.36º33´ C.36º30´30" D.36º19´48"
11.中午12点15分时,钟表上的时针和分针所成的角是( )
A. 90º B.75º C.82.5º D.60º
12.(6分)已知一条射线OA,如果从点O再引两条射线OB和OC,使∠AOB=60°, ∠BOC=20°,求∠AOC的度数.
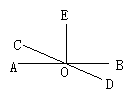
13.(8分)如图,∠AOD=∠BOC=90°,∠COD=42°,求∠AOC、∠AOB的度数. 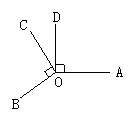
14.判断:
(1)两条不相交的直线叫做平行线 ( )
(2)同一平面内的两条直线叫平行线 ( )
(3)在同一平面内不相交的两条直线叫平行线 ( )
(4)和一条已知直线平行的直线有且只有一条 ( )
(5)经过一点,有且只有一条直线与这条直线平行 ( )
(6)a,b,c是三条直线,如果a∥b,且b∥c,那么a∥c. ( )
(7)在同一平面内的两条线段,如果它们不相交,那么它们一定互相平行.( )
(8)如果a,b,c,d是四条直线,且a∥c,c∥d,则a∥d ( )
15,在同一平面内的两条直线ab,分别根据下列的条件,写出a,b的位置关系.
(1)如果它们没有公共点,则 .
(2)如果它们都平行于第三条直线,则 .
(3)如果它们有且只有一个公共点,则 .
(4)过平面内的同一点画它们的平行线,能画出两条,则 .
(5)过平面内的不在a,b上的一点画它们的平行线,只画出一条,则
 16.过平面内一点可以作出_____条直线与已知直线垂直.
16.过平面内一点可以作出_____条直线与已知直线垂直.
17.如图,已知∠AOB=∠COD=90°,∠AOD=150°,
则∠BOC=______.
18.下列语句说法正确的个数是( )
①两条直线相交成四个角,如果有两个角相等,那么这两条直线垂直;
②两条直线相交成四个角,如果有一个角是直角,那么这两条直线垂直;
③一条直线的垂线可以画无数条;
④在同一平面内, 经过一个已知点能画一条且只能画一条直线和已知直线垂直.
A.1个 B.2个 C.3个 D.4个
19.画∠AOB,在∠AOB的内部任找一点P,
过点P画PM⊥OA于M,画PN⊥OB于N.
三、 创新应用
1.平面内画3条直线,可以把平面分成几部分
2.往返于甲、乙两地的客运火车,中途停靠三个站.(假设该车只有硬座,且各站距离不离)
(1)有多少种不同的票价;(2)要准备多少种车票?
3.木工师傅在锯木料时, 一般先在木板上画出两个点然后过这两个点弹出一条墨线,这是为什么?
4.已知:如图,B、C两点把线段AD分成2:4:3三部分,M是AD的中点,CD=6, 求线段MC的长.
![]()
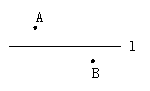
5.如图,A、B是公路L两旁的两个村庄,若两村要在公路上合修一个汽车站,使它到A、B两村的距离和最小,试在L上标注出点P的位置,并说明理由.
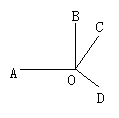
6.如图,已知O是直线AD上的点,∠AOB,∠BOC,∠COD, 三个角从小到大依次相差25度,求这三个角的度数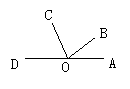 .
.
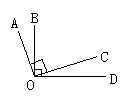
7.根据图,回答下列问题:
(1)根据∠AOB、∠AOC、∠AOD的大小,并指出图中的锐角、直角和钝角.
(2)能否看出图中某些角之间的等量关系.
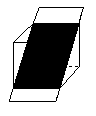
8.按图所示,所示的方法将几何体切开, 所得的三个截面有没有互相平行的线段?如果有,填上字母表示出来.
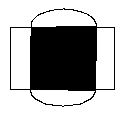
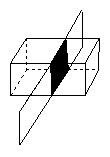
9.在下列4个判断中:
①在同一平面内,不相交也不重合的两条线段一定平行;②在同一平面内, 不相交也不重合的两条直线一定平行;③在同一平面内,不平行也不重合的两条线段一定相交;④在同一平面内,不平行也不重合的两条直线一定相交.
正确判断的个数是( )
A.4 B.3 C.2 D.1
10.请以给定的图形“○○、△△、=”(两个圆、两个三角形、两条平行线段) 为构件,构思尽可能多独特且有意义的图形,并写上一两句购切、诙谐的解说词.
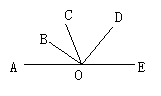
11.如图,已知A、O、E三点在一条直线上,OB平分∠AOC,∠AOB+∠DOE=90°,试问:∠COD与∠DOE之间有怎样的关系?说明理由.
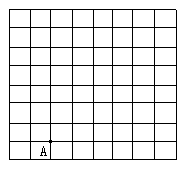
12.如图,小海龟位于图中点A处,按下述口令移动:向前前进3格;向右转90°, 前进5格;向左转90°;前进3格;向左转90°,前进6格,最后向右转90°,前进一格,用粗线将小海龟经过的路线描出来.
13.如图,OA⊥OB、OC⊥OD,OE是OD的反向延长线.
(1)试说明∠AOC=∠BOD.(2)若∠BOD=50°,求∠AOE.
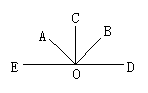
14.如图,某工厂P旁边有一条河流,在河岸AB 的什么地方建泵站抽水供工厂使用,才能尽量节约铺设的管道?请试着说出其中的理由?
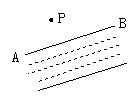
15.如图,AO⊥CO,BO⊥DO,∠BOC=30°,求∠AOD的度数.
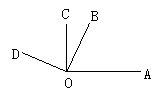
16.如图,OC⊥OB,垂足为O,∠COB与∠AOC之差为60°,试求∠AOB的度数.
(1)一变:省去图,已知条件不变.
OC⊥OB,垂足为O,∠COB与∠AOC之差为60°,试求∠AOB的度数.
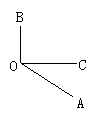
(2)二变:如图,OC⊥OB,垂足为O,∠COB:∠AOC=3:1,试求∠AOB的度数.

四、 走近中考
1.平面上有四个点,过其中每两点画直线,可以画多少条?
2.观察图中的图形,并阅读图形下面的相关文字:

像这样,10条直线相交,最多交点的个数是( )
A.40个 B.45个 C.50个 D.55个
3.三条互不重合的直线的交点个数可能是( )
A.0,1,3 B.2,3,3 C.0,1,2,3 D.0,1,2
4.如图,已知OA∥CD,OB∥CD,那么∠AOB是平角,为什么?
5、学校、电影院、公园在平面图上的标点分别是A、B、C, 电影院在学校的正东方向,公园在学校的南偏西25°方向,那么平面图上的∠CAB等于( )
A.115° B.155° C.25° D.65°
6.如图,AB、CD相交于点O,OB平分∠DOE,若∠DOE=60°, 则∠AOC的度数是_______.
7.如图,O为直线AB上一点,∠AOC=![]() ∠BOC,OC是∠AOD的平分线.
∠BOC,OC是∠AOD的平分线.
(1)求∠COD的度数; (2)试判断OD与AB的位置关系.
8.在测量跳远成绩时,从落地点到起跳线拉的皮尺应当与起跳线________.
9.如图,直线AB与CD交于O,EO⊥AB于O,∠AOD=150°, 则∠COE=_____.