初一数学自测练习题
一. 填空题（3分×10）
1. 比
的3倍与
的立方的和少3的数，用代数式表示是
。
2. 最大的负整数是 ；最小的自然数是 ；平方小于20的所有整数的和是 。
3. 
的相反数是
，绝对值是
，倒数是
。
4. 近似数3.4万精确到 位，它有 个有效数字；用四舍五入法对10410保留两个有效数字，近似值约等于 。
5. 一个数的平方等于225，这个数是 ；六次方等于它本身的数有 ，九次方等于它本身的数有 。
6. 
的最小值是
，此时的值等于
。
7. 比较有理数
的大小，若用“
”号把它们连接起来是
。
8. 纳米是很小的长度单位，1米是1纳米的十亿倍，用科学记数法表示
1米= 纳米。
9. 已知
且
，则
。
10. 直接写出计算结果：
二. 选择题（3分×10）
11. 在
，
，
，
，
，
，
中，整数和负分数一共有（ ）个。
A. 3 B. 4 C. 5 D. 6
12. 已知
，用
、
表示
与
的差为（ ）
A. 
B. 
C. 
D. 
13. 两个不为零的有理数相除，如果交换它们的位置商不变，那么这两个数的关系一定是（ ）
A. 相等 B. 互为倒数 C. 互为相反数 D. 相等或互为相反数
14. 下列式子：
，
，
，
，
，，
其中代数式的个数是（ ）
A. 7 B. 6 C. 5 D. 4
15. 一根绳子剪去三分之一后，长1.5米，这根绳子原来长是多少？设原长为米，列出的方程是（ ）
A. 
B. 
C. 
D. 
16. 数轴上有一点A，它表示有理数3，现将A向右移动2个单位到B点，再由B点向左移动9个单位到达C点，则C点表示的数是（ ）
A. 
B.
4
C. 
D.
17. 若
，
，与异号，则
的值为（ ）
A. B.
8
C. 
D.
2
18. 已知
，当
时，
，那么当
时，
（ ）
A. 20 B. 3 C. 16 D. 24
19. 已知
，化简
的结果是（ ）
A. B.
2
C. 
D.
20. 、是两个有理数，且
，
，下列图中能表示、正确位置关系的是（ ）
三. 解答题（40分）
21. 解下列方程（3分×2）
（1）
（2）
22. 计算（能简算的简算）（4分×4）
（1）
（2）
（3）
（4）
23. 仓库原有大米12吨，第一天运进55吨，第二天运出18吨，第三天运出24吨，第四天运进3吨，第五天运出26吨，运用有理数加法法则列式计算仓库里还存多少大米？（本题4分）
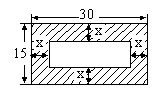
24. 根据在图中的尺寸（单位：米），
（1）写出阴影部分的面积
的计算公式。
（2）求当
米时的值。（本题4分）
25. 已知，
，
，且
，
，求：
的值。（本题5分）
26. 已知：
求：
的值。（本题5分）
【试题答案】
一.
1. 
2. 
；0；0 3. 
；；
4. 千；2；
5. 
；1，0；
，0 6. ；3 7. 
8. 
9. 10. 
；
；
二.
11—15 CCDCD 16—20 ABDBB
三.
21.
（1）解： 
（2）解： 
22.
（1）解：原式
（2）解：原式
（3）解：原式
（4）解：原式
23. 解：规定运进为正，则有
=
答：仓库里还存2吨大米。
24. 解：
（1）S
（2）当时，
答：当米时，阴影面积S为350平方米。
25. 解：由已知得
，
，
∵ ∴ 
或
∵ 
∴ 
当
时，
当
时，
∴ 的值为或
26. 解：由题意得，
且
∴ 
∴ 原式
【励志故事】
名气的价值
美国南北战争结束后，太平洋人寿保险公司拟以3万美金的年俸，聘请曾任南部联军统帅的名将李将军为该公司董事长，但遭李将军拒绝，理由是他对人寿保险业务毫无心得。公司负责人当即告称：“阁下对人寿保险业务无心得无所谓，我们需要的是您的大名。”
“好的，可见我的名气很有价值，”李将军严肃地说，“正因为此，今天我不得不告诉你，我要把它用在与它价值相配的地方。”
后来，李将军欣然接受了一个小规模专科学校校长的职务，年薪只有1500美元。
30000＜1500，这在数学上是谬误，但在李将军那里却是名气的价值。于是我们便不难明白李将军为何在美国颇受尊敬，因为一个真正伟大睿智的人知道什么才是真正的价值，更知道如何找到价值的归属。