《三角形的初步认识》测试卷
姓名___________
一、填空题 (30分) ：
1、在Rt△ABC中,一个锐角为250, 则另一个锐角为________；
2、 在△ABC中，AB＝3，BC＝7，则AC的长x的取值范围是________；
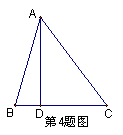
3、如图,AD是△ABC的中线, △ABC的面积为100cm2,则△ABD的面积是______cm2；
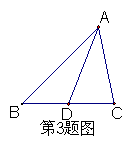
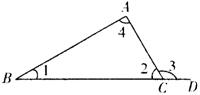
4、如图, △ABC中, ∠ABC=740,AD为△ABC的高,则∠BAD=_______；
5、如图, △ABC中,AB=12,EF为AC的垂直平分线,若EC=8,则BE的长为_______；
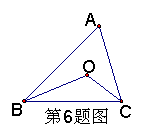
6、如图, △ABC中,∠ABC和∠ACB的平分线交于点O,若∠A=700,则∠BOC=_______；
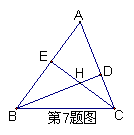
7、如图, △ABC中,高BD、CE相交于点H,若∠A=600,则∠BHC=_____；
 |
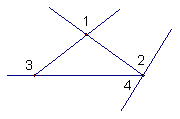
8、 如上右图，∠1∶∠2∶∠3＝1∶2∶3，则∠4＝________；
9、已知△ABC中, ∠A=
∠B=
∠C,则△ABC为___________ 三角形；
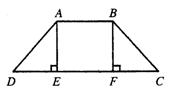10、 如图，四边形ABCD是一防洪堤坝的横截面，AE⊥CD，BF⊥CD，且AE=BF，∠D=∠C，问AD与BC是否相等？说明你的理由。
解：在△ADE和△BCF中，
∠D=∠C (
)
∠AED=∠ (垂直的意义)
AE=BF （ ）
∴△ADE≌△BCF (_______ )
∴AD=BC (______________________)
二、选择题(30分)：
1、以下列各组线段为边，能组成三角形的是( )；
A．2cm、2cm、4cm B．2cm、6cm、3cm
C．8cm、6cm、3cm D．11cm、4cm、6cm
2、 有下列关于两个三角形全等的说法: ㈠三个角对应相等的两个三角形全等;㈡三条边对应相等的两个三角形全等;㈢两角与一边对应相等的两个三角形全等;㈣两边和一角对应相等的两个三角形全等.其中正确的个数是（ ）；
A.1 B.2 C.3 D.4
3、如右图,三角形的外角是( )；
A. ∠1 B.∠2 C.∠3 D.∠4
4、若三角形的一个外角小于和它相邻的内角,则这个三角形为( )；
A.锐角三角形 B.钝角三角形 C. 直角三角形 D无法确定
5、对于三角形的内角,下列判断中不正确的是( )；
A.至少有两个锐角 B.最多有一个直角
C.必有一个角大于600 D.至少有一个角不小于600
6、下列四组中一定是全等三角形的是( )；
A．两条边对应相等的两个锐角三角形 B．面积相等的两个钝角三角形
C．斜边相等的两个直角三角形 D．周长相等的两个等边三角形
7、若AD是△ABC的中线,则下列结论错误的是( )；
A.AD平分∠BAC B.BD=DC C.AD平分BC D.BC=2DC
8.如果三角形的一个内角等于其他两个内角的差,那么这个三角形是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
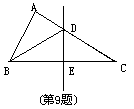9. 如图,在ΔABC中,BC边上的垂直平分线交AC于点D,
已知AB=3,AC=7,BC=8,则ΔABD的周长为:
A.10 B.11 C.15 D.12
10.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是 ( )
A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定
三、解答题(6+8+8+8+10=40分)：
1、如图,在⊿ABC中, ∠BAC是钝角,按要求完成下列画图,并用适当的符号在图中表示（必须写出结论）：
①∠BAC的角平分线
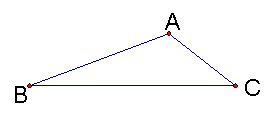②AC边上的高
③AB边上的中线
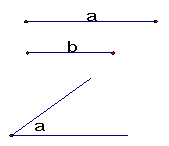2、尺规作图：已知线段a,b和∠α.
求作:ΔABC,使BC=a , AC=b , ∠C=∠α
(画出图形,保留作图痕迹,不写作法,写出结论)
3、如图：已知△ABC中，AD⊥BC于D，AE为∠BAC的平分线，且∠B=35°，
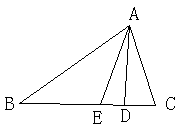∠C=65°求∠DAE的度数。
4、如图,已在AB=AC,AD=AE, ∠1=∠2,试说明ΔABD≌ΔACE的理由.
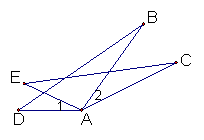解：∵∠1=∠2（ ）
∴∠1+∠ =∠2+∠
即：∠BAD=∠CAE
在△BAD和△CAE中
AB=AC（
）
∠BAD=∠CAE
AD=AE（ ）
∴△BAD≌△CAE( )
5、如图．在△ABC和△DEF中，B、E、C、F在同一直线上，下面有四个条件．请你在其中选三个作为已知条件，余下的一个作为结论，写出—个正确的结沦，并说明理由。 ①AB＝DE；②AC＝DF；③∠ABC＝∠DEF；④BE＝CF．（填写序号即可）
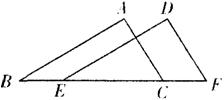已知：
；
结沦： ；
理由：
四、附加题（9+11=20分）：
1、设计三种不同方案，把ΔABC的面积三等分
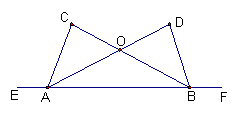
2、如图,点E、A、B、F在同一条直线上,AD与BC交于点O,已知∠CAE=∠DBF,AC=BD.
说出∠CAD=∠DBC的理由
参考答案：
一、填空题：
1、650
2、4＜x＜10
3、50
4、160
5、4
6、1250
7、1200
8、720
9、直角
10、已知，BFC，已知，AAS，全等三角形的对应边相等。
二、选择题：
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 答案 | C | A | C | B | C | D | A | C | A | C |
三、解答题：
1、（略）.
2、（略）.
3、150.
4、已知，BAE，BAE，已知，已知，SAS.
5、答案不唯一.
四、附加题：
1、（略）；
2、解：∵∠CAE=∠DBF（已知）
∴∠CAB=∠DBA（等角的补角相等）
在△ABC和△DBA中
AC=BD（已知）
∠CAB=∠DBA
AB=BA（公共边）
∴△ABC≌△DBA（SAS）
∴∠ABC=∠BAD（全等三角形的对应角相等）
∴∠CAB-∠BAD=∠DBA-∠ABC
即：∠CAD=∠DBC