七年级数学规律探索问题

第七讲　 七年级数学规律探索问题

一、数与式规律:

1. 观察下列等式：

=1－， ， ，……

请根据上面的规律计算：____________.

2.根据规律填代数式，

1+2=;……

1+2+3+…+n=______________.

3.根据规律填代数式，

1³+2³=(1+2)²

1³+2³+3³=(1+2+3)²

1³+2³+3³+4³=(1+2+3+4)²

……

1³+2³+3³+…+n³=　　　　　　　　  .

4、（2007内蒙古赤峰）观察下列各式：

……

依此规律，第个等式（为正整数）为　　　　 

二、图形的规律:

1、（2007浙江温州）意大利著名数学家斐波那契在研究兔子繁殖问题时，发现有这样一组数：1，1，2，3，5，8，13，…，

其中从第三个数起，每一个数都等于它前面两上数的和。现以这组数中的各个数作为正方形的长度构造如下正方形：

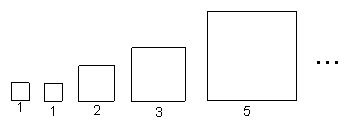
序号	①	②	③	④
周长	6	10	16	26

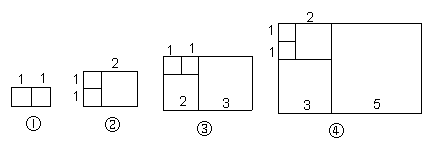再分别依次从左到右取2个、3个、4个、5个,正方形拼成如下矩形并记为①、②、③、④.相应矩形的周长如下表所示：

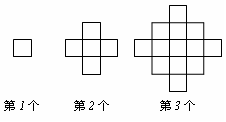
2、（2007湖北武汉）下列图案是由边长为单位长度的小正方形按一定的规律拼接而成。依此规律，第5个图案中小正方形的个数为_______________。

3、（2007哈尔滨）柜台上放着一堆罐头，它们摆放的形状见右图：

第一层有听罐头，

第二层有听罐头，

第三层有听罐头，……

根据这堆罐头排列的规律，第（为正整数）层有　　　　 听罐头（用含的式子表示）．　

4、（2007湖南湘潭）为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：

按照上面的规律，摆个“金鱼”需用火柴棒的根数为（　　）

A．　　　　　 B．　　　　　　　 C．　　　　　　D．

三.整式的应用:

1.销售问题：某商场将进价a元的货物提价40%后销售，后因积压又按售价的60%出售，用代数式表示实际的售价，问这次是亏了还是赚了？

2.放射性物质的原子数从开始存在到衰变成一半所需的时间叫做半衰期.如某元素的半衰期为2000年，就是说，现在该元素的原子个数为，经过2000年后原子个数变为.经测定一个动物化石中该元素的原子个数为c，而同等条件下正常的活动物体内该元素的原子个数为16c，请你估计以下这个化石的年龄大约是多少？

3.(1)正方形的周长为m，正方形的面积是_______，圆的周长为m，圆的面积是_______.

(2)同样长的两段铁丝，一个做成正方形框架，另一个做成圆形框架，请你判断，哪个框架的面积更大一些？

4.一张长为a宽为b的铁板(a＞b)，从四个角截去四个边长为x的小正方形 ，做成一个无盖的盒子，用代数式表示：

(1)无盖盒子的外表面积；（用两种方法）

(2)无盖盒子的容积.

5.m为何值时，代数式的值是自然数.

6.比较和的大小（是自然数），我们从分析，，这些简单情况入手，从中发现规律，经过归纳，再猜出结论．

（1）通过计算，比较下列各组中两个数的大小（在空格内填写">""="或"<"）

①　　②　 ③　　④　⑤

（2）从第（1）题结果归纳，可猜出与的大小关系是　　　　　 .

7、（2007浙江杭州）如图，是一块半径为1的半圆形纸板，在的左下端剪去一个半径为的半圆后得到图形，然后依次剪去一个更小的半圆（其直径为前一个被剪掉半圆的半径）得图形，记纸板的面积为，试计算求出　　　　；　　　　；并猜想得到　　　 　　 。
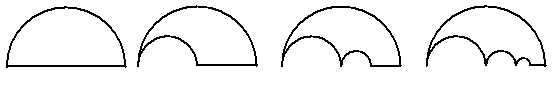