第三章《一元一次方程》素质提高
练习二 一元一次方程的讨论及实际运用
一、精心选一选
1、下列说法中正确的是( )
A、合并χ-3χ得2χ
B、合并![]()
C、χ= -3是方程χ-3=0的解 D、以上说法都不对
2、方程(a-1)x2-ax+1=0是一元一次方程,则a等于( )
A、0 B、1 C、±1 D、-1
3、若关于χ的aχ=3的解是自然数,则整数a的值为( )
A、1 B、3 C、1或3 D、±1或±3
4、方程2χ-kχ+1=5χ-2的解是-1时,k的值为( )
A、-4 B、-6 C、-8 D、10
5、从一块正方形木块上锯掉2米宽的长方形木条,剩下面积是48平方米,则原来这块木板面积是( )
A、150平方米 B、52平方米 C、64平方米 D、136平方米
6、解方程![]() 时,去分母后,结果正确的是(
)
时,去分母后,结果正确的是(
)
A、2χ+1-8χ+2=6 B、2χ+1-8χ-2=6
C、2χ+1-8χ+2=1 D、2χ+1-8χ-2=1
二、细心填一填
1、如果-2a=4b,那么a=________,a+2b=_________。
2、方程aχ=b的解是χ=![]() 的条件是_____________。
的条件是_____________。
3、香蕉和苹果的售价分别是3元/千克、5元/千克,现在小明手中共33元钱,要买香蕉和苹果共9千克,请你帮小明算一算,买香蕉______________千克,买苹果____________千克。
4、某商品的进价为a元,售价为b元,则利润为_________。
5、一架飞机在静风中的速度为1200千米/时,在风速为χ千米/时中飞行,顺风速度为________,逆风速度为______________.
6、甲用40秒跑完一环形跑道,乙反向跑,每隔15秒与甲相遇一次,那么乙跑完这个跑道需要__________秒。
7、甲、乙两个工程队合修一条长为10公里的公路,甲队每天修40米,乙队每天修60米,若设完成这项工程需χ天,那么可得方程______________.
三、耐心做一做
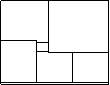
1、如图为一块在电脑屏幕上出现的色块图,由6个颜色不同的正方形拼成的长方形,如果中间最小的正方形边长为1,求所拼成的长方形的面积。
 |
2、商场计划拨款93元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案。
(2)若商场销售一台甲种电视机可获利150元,销一台乙种电视机可获利200元,销售一台丙种电视机获利250元,那么你会选择哪种进货方案?
参考答案
一、1、B 2、B 3、C 4、B 5、C 6、B
二、1、-2b,0 2、a≠0 3、6,3 4、(b-a)元 5、(1200+χ)千米/时,(1200-χ)千米/时 6、24 7、40χ+60χ=10000
三、解:设右下方两个并排的正方形的边长为χ,则χ+2+χ+1=2χ-1+χ
χ=4,所以长方形长为3χ+1=13,宽为3χ-1=11,面积为13×11=143。
2、(1)方案一:进甲种电视机χ台,乙种(50-χ)台,
则1500χ+(50-χ)×2100=90000
χ=25,50-χ=25
故甲、乙两种电视机各进25台。
方案二:进甲种电视机у台,丙种(50-у)台,
则1500у+(50-у)×2500=90000,
у=35,50-у=15
故甲种进35台,丙种15台。
方案三:进乙种电视机z台丙种(50-z)台。
则2100z+(150-z)×2500=90000,
Z=87.5(舍去)
因此有两种进货方案。
(2)获利情况:
方案一:150×25+200×15=8750(元)
方案二:35×150+15×250=9000(元)
因为:8750<90000,
所以应选择方案二进货。![]()