第一章《有理数》 章末总结
一、正数和负数
1．负数 像-3，-2，-0.5这样除0以外的数前面加上______“－”的数.
2．正数 像3，2，+0.5这样除0以外的数，它们与_______具有相反的意义．
3．0既不是_______，也不是________，它是正数与负数的______，0的意义已不仅是表示“_______”．
二、有理数
1．整数 ________、0、______统称整数．
2．有理数 _________和________统称有理数．
3．数轴 通常用_______上的点表示数，这条________叫做数轴，它满足以下要求：（1）在直线上任取一点表示________，这个点叫做__________．（2）通常规定直线上从_________向_________（或上）为_________方向，从原点向________（或向下）为_________方向．（3）选取适当的长度为__________．一般地，设a为一个正数，则数轴上表示数a的点在原点的________边，与原点的距离是______个单位长度；表示-a的点在原点的________边，与原点的距离_________个单位长度．
4．相反数 像2和-2，5和-5这样，只有_______不同的两个数叫做互为相反数，一般地，a和______互为相反数，特别地，0的相反数是_____．数轴上表示相反数的两个点关于________对称．
5．绝对值 一般地，数轴上表示数a的点与______的距离叫做数a的绝对值，记作_______，由绝对值定义可知：一个正数的绝对值是它______；一个负数的绝对值是它的______；0的绝对值是________．
（1）当a是正数时，│a│=________; （2）当a是负数时，│a│=________．
（3）当a=0时，│a│=________．
6．有理数大小比较法则
（1）正数大于_______，0大于________，正数大于负数；
（2）两个负数，绝对值大的反而_________．
三、有理数的加减法
1．有理数加法法则
（1）同号两数相加，取________的符号，并把________相加．
（2）绝对值不相等的______两数相加，取______的加数的符号，并用_____减去______，互为相反数的两个数相加得________．
（3）一个数同_______相加，仍得______．
2．有理数加法的运算律
（1）加法的交换律：两个数相加，交换________的位置，_______不变，即a+b=_____．
（2）加法的结合律：三个数相加，先把前两个数______，或者先把后两个数_______，和_______，即（a+b）+c=_______．
3．有理数减法法则 减去一个数，等于_______这个数的______，即a-b=a+_______．
四、有理数的乘除法
1．有理数的乘法法则 两数相乘，同号得_______，异号得_______，并把_______相乘，任何数同_____相乘，都得________．
2．乘积是_______的两个数互为________．
3．几个不为0的数相乘，负因数的个数是_______时，积是正数；负因数的个数是_________时，积是负数．
4．有理数乘法的运算律
（1）乘法交换律：两个数相乘，交换________的位置，________相等，即ab=____．
（2）乘法结合律：三个数相乘，先把前两个数______，或者先把后两个数_______，再把_______相加．即a（b+c）=_______．
5．分配律
一般地，合并含有字母相同因数的式子时，只需将它们的_______合并，所得结果作为______，再乘字母_______．即ax+bx=________x．
6．去括号
括号外的因数是_______，去括号后式子各项的符号与原括号内式子相应各项的符号__________；括号外的因数是______，去括号后式子各项的符号与原括号内式子相应各项的符号________．
7．有理数的除法法则
除以一个不等于________的数，等于________这个数的________，同号得_____，异号得______，并把绝对值_______，0除以任何一个不等于0的数，都得_______．
8．有理数加减乘除混合运算顺序
如无括号指出，则按照“________”的顺序进行．
五、有理数的乘方
1．乘方定义 求n个______的积的运算，叫做乘方．________叫做幂，在a中，_______叫做指数，_______叫做底数．
2．有理数乘方法则 负数的________是负数，负数的偶次幂是_________，正数的任何次幂都是________，0的任何_________都是0．
3．有理数的混合运算顺序
（1）先_______，再_____，最后_________．
（2）同级运算，从_________到__________进行．
（3）如有括号，先做括号内的运算，按_______，________，_______依次进行．
4．科学记数法 把一个大于________的数表示成________的形式（其中a是_______只有______的数，n是________）．
在科学记数法中，符号_______整数的_______比右边10的指数多________．
5．有效数字 从一个数的_________第一个________数字起，到________数字止，所有数字都是这个数的有效数字．
答案:
一、
1．负号 2．负数 3．正数 负数 分界 没有
二、
1．正整数 负整数 2．整数 分数
3．一条直线 直线 （1）0 原点 （2）原点 右 正 左 负
（3）单位长度 右 a 左 a 4．符号 -a 0 原点
5．原点 │a│ 本身 相反数 0 （1）a （2）-a （3）0 6．（1）0 负数 （2）小
三、
1．（1）相同 绝对值 （2）异号 绝对值较大 较大的绝对值 较小的绝对值 0
（3）0 这个数
2．（1）加数 和 b+a （2）相加 相加 不变 a+（b+c）
3．加上 相反数 （-b）
四、
1．正 负 绝对值 0 0 2．1 倒数 3．偶数 奇数
4．（1）因数 积 ba （2）相乘 相乘 积 a（bc） （3）相乘 和 ab+ac
5．系数 系数 因数 （a+b）
6．正数 相同 负数 相反
7．0 乘以 倒数 正 负 相除 0
8．先乘除，后加减
五、
1．相同因数 乘方的结果 n a
2．奇次幂 正数 正数 正整数次幂
3．（1）乘方 乘除 加减 （2）左右 （3）小括号 中括号 大括号
4．10 a×10n 整数数位 一位 正整数 左边 位数 1
5．左边 非0 末位
第一章《有理数》测试题
（时间90分钟 满分120分）
一、选择题（每小题5分，共40分）
1．下列四个数中，在-2和0之间的数是（ ）
A．-1 B．1 C．-3 D．3
2．│-5│的相反数是（ ）
A．-5
B．-
C．5
D．±5
3．-
的倒数是（ ）
A．8 B．-8 C．
D．-
4．-72的值是（ ）
A．-49 B．49 C．-14 D．14
5．下列计算57×99+44×99-99正确的是（ ）
A．99×（57+44）=99×101=9999 B．99×（57+44-1）=99×100=9900
C．99×（57+44+1）=99×102=10098 D．99×（57+44-99）=99×2=198
6．计算（-4）×（-
）的结果是（ ）
A．8 B．-8 C．2 D．-2
7．如果水位下降3m记作-3m，那么水位上升4m记作（ ）
A．1m B．7m C．4m D．-7m
8．
（ab≠0）的所有可能的值有（ ）
A．1个 B．2 C．3个 D．4个
二、填空题（每小题5分，共45分）
9．观察下列一组数据，按某种规律在横线上填上适当的数：-5，-2，1，4，_____，10．
10．一个点从数轴上的原点开始，先向右移动1个单位长度，再向左移动2个单位长度，这时它表示的数是_______．
11．早春二春的某一天，大连市南部地区的平均气温为-3℃，北部地区的平均气温为-6℃，则当天南部地区比北部地区的平均气温高_______℃．
12．以下是一个简单的数值运算程序： 输入x → x（-3） → -2 →输入 ．当输入x的值为-1时，则输出的数值为________．
13．已知9×1+0=9，9×2+1=19，9+3+2=29，9×4+3=39，…，根据前面式子构成的规律写出第6个式子是________．
14．已知数x，y满足（x+4）+│y-1│=0，则x+y=________．
15．观察下列球的排列规律（其中●是实心球，○是空心球）．
●○○●●○○○○○●○○○●●○○○○○●○○●●○○○○○●…
从第1个球起到第2004个球止，共有实心球________个．
16．据中新社报道：2010年我国粮食产品将达到千克．用科学记数法表示为________千克．
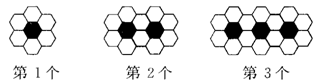
17．用黑白两种颜色的正六边形地面砖按如图1-23所示的规律拼成若干个图案．
（1）第4个图案中有白色地面砖_______块;（2）第n个图案中有白色地面砖_______块．
三、计算题（每小题7分，共35分）
18．计算-4+（-3
）+（+6）+（-2
）; 19．计算（-64）÷（-
．
20．计算32÷（-3）2+│
│×（-6）+7．
21．在数轴上画出表示数│-3│，-2，-4的点，把这组数从小到大用“<”号连接起来．
22．如果│ab-2│+（b-1）2=0，试求:
的值．
答案:
1．A
2．A [提示：-│-5│=-5．]
3．B [提示：-的倒数是1÷（-）=-8．]
4．A [提示：-72的表示的意义是72的相反数．]
5．B [提示：逆用乘法分配律．]
6．C [提示：先确定符号为正，再求绝对值．]
7．C [提示：水位下降记为负，那么上升就记为正．]
8．C [提示：因为ab≠0，所以a≠0，b≠0，当a>0，b>0时，=
=1+1=2．
当a>0，b<0时，=
=1-1=0．
当a<0，b>0时，=
=-1+1=0．
当a<0，b<0时，=
=-1-1=-2．]
9．7 [提示：通过观察可知后面每个数都比其前一个数大3，故选C．]
10．-1 [提示：画数轴分析即可．]
11．3 [提示：根据题意可得-3-（-6）=-3+6=3．]
12．1 [提示：由图可知，输出的式子为-3x-2，当x=-1时，-3x-2=-3×（-1）-2=3-2=1．]
13．9×6+5=59 [提示：根据前面式子得到的规律是9n+（n-1）．]
14．-3 [提示：由（x+4）2≥0，│y-1│≥0，且（x+4）2+│y-1│=0，得x+4=0，y-1=0，所以x=-4，y=1，所以x+y=-4+1=-3．]
15．602 [提示：观察排列规律发现，按顺序每10个球中实心球总是3个，2000个球中有200个10，所以200×3=600个，而最后4个球的排列顺序是…
．
所以共有实心球600+2=602个．]
16．5.4×1011 [提示：10的指数比原整数数位少1．]
17．（1）18
（2）4n+2 [提示：通过观察可知第1个图形中有白色地面砖6个=4×1+2，
第2个图形中有白色地面砖10个=4×2+2，第三个图形中有白色地面砖14个=4×3+2，
所以第n个图形中有白色地面砖（4n+2）个．]
18．解：-4+（-3
）+（+6）+（-2）
=[-4+（-3）]+[+6
+（-2）]=-8+4=-3
．
19．解：（-64）÷（-
=（-64）×（-
）=-64×（-1）=64．
20．解：32÷（-3）2+││×（-6）+7=9÷9+×（-6）+7=1+（-1）+7=7．
21．解：在数轴上表示│-3│，-2，-4，如图所示．
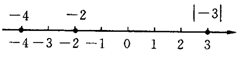
由此图可得-4<-2<│-3│．
22．解：因为│ab-2│+（b-1）2=0，且│ab-2│≥0，（b-1）2≥0，
所以ab-2=0，b-1=0，
所以b=1，a=2．
所以原式=
=1-+-+-+…+
．