七年级数学第一学期期中试题2
班级 姓名 分数
一、 填空（24）
1．圆柱体有 个面，侧面展开图是 形．
2. 举例说明代数式25a+12b的意义______________________________ .
3．-2３的底数是_______,指数是_______．
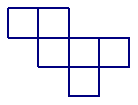4．在如图所示的六个方格中,分别填入下列各数,使围成正方体后相对两面的两个数互为倒数.(填写各数的序号即可) ．
①-2 ②4 ③
④8 ⑤
⑥
5．代数式
共有______项,其中第2项的
系数是_____ _．
6．若
与
是同类项，则m= , n= ．
7．有理数0，2，－7, 
,3.14, 
,－3, －0.75中,负整数是
,分数是
．
8．根据规律填上合适的数：(1) 1，4，9，16， ,36 ；
(2) 2，5，10，17， ，37,_____ ．
9．数轴上表示－2的点先向右移动3个单位，再向左移动5个单位，则此时该点表示的数是_____ __．
10．a的平方的一半与b平方的差,用代数式表示为___________________．。
11．已知a、b互为相反数,c、d互为倒数, 
=－3.则代数式
的值为________．
12．对有理数a、b,定义运算a*b=
,则3*4=________．
二．选一选（每题2分，共16分）
13．下列各图经过折叠后不能围成一个正方体的是……………………（ ）
A B C D
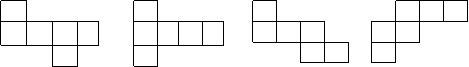
14．下列说法不正确的是…………………………………………………( )
A．1是绝对值最小的数； B．0既不是正数，也不是负数；
C．一个有理数不是整数就是分数； D．0的绝对值是0．
15．若a－b－c=a-( )成立，则括号应填入………………………（ ）
A． b－c； B． b+c； C． －b+c ； D． －b－c．
16．下面各组数中，相等的一组是…………………………………………( )
A．
与
； B．
与
；C．
与
； D．
与
．
17．观察下列算式：
，
，
，则a、b、c的大小关系是……………………………………………………………（
）
A．b>c>a； B．a >c>b ； C．a>b>c； D． c>b>a．
18．若
，则
的值为……………………………（ ）
A．1 ； B. －1 ； C. 3； D. －3．
19、某商店进了一批商品，每件商品的进价为a元，若要获利20%，则每件商品的
零售价定为（ ）
A、20%a元 B、（1-20%）a元 C、
元 D、（1+20%）a元
20、下列各式正确的是（ ）
A. －32 =9 B. －(－3)2=9 C. －23 = －8 D. －(－2)3= －8 三．解解看
21．如图所示是由几个小立方块所搭的几何体的俯视图，小正方形中的数字表示在该位置小立方块的个数，请画出相应几何体的主视图和左视图：4’
22．有理数运算．16’
（1）[12-（3-10）×4] ÷4
(2)
（3）
(4)-32÷（-3）2+3×（-6）
23.把表示下列各数的点画在数轴上，再按从小到大的顺序，用“＜”号将这些数
连接起来。4’
2.5 -3 
0 -1.5
-4 -3 -2 -1 O 1 2 3 4 5 6
24．化简、求值，列式计算．16’
（1）
(2) 当a＝-2，b=5时，求代数式
的值。
（3）被减式是
，差是
，求减式是多少？
（4）5(3x2y—5xy2)—(xy2+3x2y)， 其中x= 1, y=－1
25．某空调器销售商，今年四月份销出空调（a-1）台，五月份销售空调比四月份的2倍少1台，六月份销售空调比前两个月的总和的4倍还多5台．4’
（1）用代数式表示该销售商今年第二季度共销售空调多少台？
（2）若a=220，求第二季度销售的空调总数．
26.我国出租车收费标准因地而异. A市为：起步价10元，3千米后每千米价为1.2元；B市为：起步价8元，3千米后每千米价为1.4元. 试求：4’
(1) 在A、B两市乘坐出租车x（x>3）千米的花费分别是多少元？
(2) 若某乘客需在A、B两市乘坐出租车各12千米，你认为哪个城市出租车收费较便宜？若某乘客需在A、B两市乘坐出租车各15千米呢？
27． “十.一”黄金周期间，某风景区在7天假期中每天旅游的人数变化如下表（正数表示比前一天多的人数，负数表示比前一天少的人数）： 4’
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 人数变化(万人) | ＋1.6 | ＋0.8 | ＋0.4 | －0.4 | －0.8 | ＋0.2 | －1.2 |
(1)若9月30日的游客为3万人，请完成下面7天游客人数记录表：
| 日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 游客人数 (万人) | 4.6 |
(2)七天内游客人数最多的一天有 万人；游客人数最少的一天是第 天．
28．树的高度与树生长的年数有关，测得某树的有关数据如下表（树苗原高100厘米）：
| 年数a | 高度h（单位：厘米） |
| 1 | 115 |
| 2 | 130 |
| 3 | 145 |
| 4 | |
| … | …… |
（1）填出第4年树苗可能达到的高度；
（2）请用含a的代数式表示： a年后树的高度h=____ ________；
（3）根据这种长势，10年后这棵树可能达到的高度是 厘米．
29.1是个正五边形，分别连接这个正五边形各边中点得到图2，再分别连接图2小正五边形各边中点得到图3：6’
图１ 图2 图3
1、填写下表：
| 图形标号 | 1 | 2 | 3 |
| 正五边形个数 | |||
| 三角形个数 |
2、按上面方法继续连下去，第n个图中有多少个三角形？
3、能否分出246个三角形？简述你的理由。