七 年 级 数 学 试 卷
班级 学号 姓名
一、填空题 （每小题2分，共20分）
1、 计算： -22+20--3×(-3)-1 = ； 
。
2、中国宝岛台湾面积约3.5万平方公里，人口约2227.60万人，你认为人口数是精确到
位，有效数字有 个。
3、小红将一张正方形的红纸沿对角线对折后，得到等腰直角三角形，然后在这张重叠的纸上剪出一个非常漂亮的图案，她拿出剪出的图案请小冬猜，打开的图案至少有
条对称轴，至多有 条对称轴。
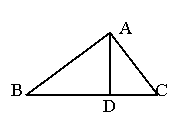
4、如图，AD是Rt△ABC斜边BC上的高，与∠B相等的角是 ，理由是 。
5、（画图）把△ABC分成面积相等的两部分，把△DEF分成面积相等的四部分。
（第5题） （第8题）
6、等腰三角形一边的长是4，另一边的长是8，则它的周长是 。
7、已知，等腰三角形一内角等于70°，则它的顶角为 。
8、在平面镜里看到背后墙上，电子钟示数如图所示，这时的时间应是 。
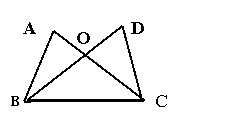
9、如图，已知AC=BD,要使△ABC≌△DCB，
只需增加一个条件是 。
|
（第4题） （第9题） （第10题）
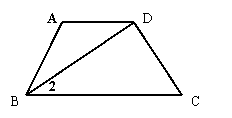
10、如图，已知AD//BC，∠1=∠2，∠A=112°，且BD⊥CD，则∠ABC=_____，∠C=_____.
二、选择题：（每题2分，共12分）
11、下列运算正确的是（ ）。
A 
B
C 
D
12、给出下列图形名称：（1）线段 （2）直角 （3）等腰三角形 （4）平行四边形 （5）长方形，在这五种图形中是轴对称图形的有（ ）
A 1个 B 2个 C 3个 D 4个
13、一只小狗在如图的方砖上走来走去，最终停在阴影方砖上的概率是（ ）
A 
B 
C
D 
14、1纳米相当于1根头发丝直径的六万分之一。则利用科学记数法来表示，头发丝的半径是（ ）
A 6万纳米 B 6×104纳米 C 3×10－6米 D 3×10－5米
15、下列条件中，能判定两个直角三角形全等的是（ ）
A 一锐角对应相等 B 两锐角对应相等
C 一条边对应相等 D 两条直角边对应相等
16、如图，下图是汽车行驶速度（千米／时）
和时间（分）的关系图，下列说法其
中正确的个数为（ ）
（1）汽车行驶时间为40分钟；
（2）AB表示汽车匀速行驶；
（3）在第30分钟时，汽车的速度
是90千米／时；
（4）第40分钟时，汽车停下来了．
A 1个 B 2个 C 3个 D 4个
三、计算题：（3分+3分+4分=10分）
17、
18、
解：原式＝ 解：原式＝
19、
其中
解：原式＝
 |
四、解答题
20、看图填空：（5分）
已知：如图，BC∥ EF，AD=BE，BC=EF
试说明 △ABC ≌ △DEF
解：∵AD=BE ∴＿＿＿=BE+DB
即：＿＿＿=＿＿＿ ∵BC∥ EF
∴∠＿＿＿=∠＿＿＿（ ）
在△ABC和△DEF中
＿＿＿＿＿＿＿＿＿
＿＿＿＿＿＿＿＿＿ ∴△ABC ≌ △DEF（SAS）
＿＿＿＿＿＿＿＿＿
21、如图，△ABC中，AB=AC，∠A=36°，DE垂直平分AB，
△BEC的周长为20，BC=9
（1） 求∠ABC的度数；（3分）
解：
|
（2） 求△ABC的周长（3分）
解：
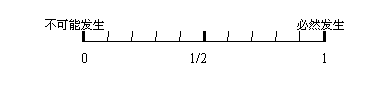
22、请将下列事件发生的可能性标在图中（把序号标出即可）：(4分)
（1）7月3日太阳从西边升起；
（2）在20瓶饮料中，有2瓶已过了保质期，从中任取一瓶，恰好是在保质期内的饮料；
（3）在5张背面分别标有“1”“2”“3”“4”“5”的形状完全一样的卡片中任取一张恰好是“4”的卡片；
（4）在数学活动小组中，某一小组有3名女生、2名男生，随机地指定1人为组长，恰好是女生。
五、阅读操作题（请同学们耐心、仔细阅读，思考作答）（7分）
23、某中学七年级某班学生小明，在学习了统计图的制作和变量的关系的知识后，想给自己制作一张反映自己学习成绩成长趋势的统计图，以了解自己学习成绩的变化趋势。
|
|
小明兴冲冲地把自己的想法告诉了数学老师，数学老师高度表扬了小明，认为小明是个爱动脑筋且能活学活用、有创新意识的孩子，如果能够持之以恒，前途不可限量。小明很快从老师那儿拿到了自己的各次考试成绩，以及相应的班级各次平均分，请你帮小明算出他的各次成长分值，以及帮小明画出他的成长趋势图。
|
| 第一章 | 第二章 | 第三章 | 第四章 | …… |
| 考试成绩X | 73 | 85 | 84 | 93 |
|
| 班级平均分Y | 63 | 70 | 64 | 68 |
|
| 成长分值A A=X－Y+60 |
|
|
|
|
解：（1）小明应制作 统计图才能反映成绩的变化趋势；
（2）因变量是 ；
（3）填出上表的各章考试的成长分值，并画出小明的成长趋势图：
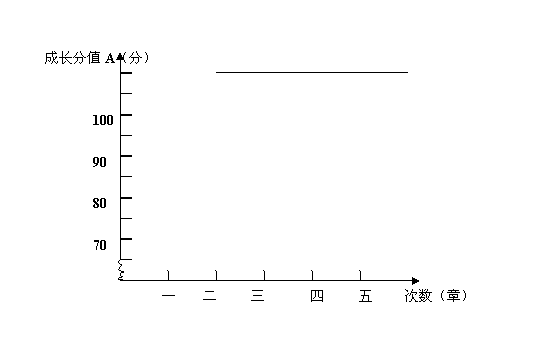
（4）按照小明的成长趋势，请你预测小明第五章的成长分值A是 分。
理由是
。
六、探究题（6分）
24、如图：E在线段CD上，EA、EB分别平分∠DAB和∠CBA,
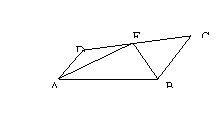∠AEB=90° ， 设AD＝
BC＝
且
（1）求AD和BC的长；
（2）你认为AD和BC还有什么关系？并验证你的结论；
（3）你能求出AB的长度吗？若能，请写出推理过程；若不能，请说明理由。