4.8平行线
一、填空.
1.______________________________________,不相交的两条直线叫做平行线.
2.在同一平面内,两条直线(不重合)的位置关系有_____种,它们是_______________.
3.经过已知直线外一点,有且只有______条直线与已知直线平行.
4.平行于同一直线的两条直线(不重合)的位置关系是__________________.
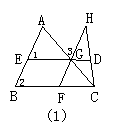
5.如图1,(1)如果∠1=∠2,根据___________________________________,得DE∥BC;
(2)如果∠2+∠BED=180°,根据_______________________________,得DE∥BC;
(3)如果∠EGF=∠GFC,根据____________________________________,得DE∥BC;
(4)如果AB∥GF,根据________________________________________,得∠2=∠GFC;
(5)如果AB∥GF,根据______________________________________,得∠A+∠FGA=180°;
(6)如果AB∥GF,根据_______________________________________,得∠A=∠3.
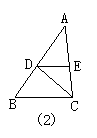
6.如图2,已知CD平分∠ACB,DE∥BC,∠AED=80°,则∠EDC=________.
7.不相邻的两个直角,如果它们有一条公共边,那么另两条边相互_______.
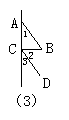
8.如图3,已知AB∥CD,∠1=43°,∠2=47°,则∠B=________,∠ACB=_______.
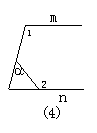
9.如图4,已知m∥n,∠1=105°,∠2=140°,则∠α=________.
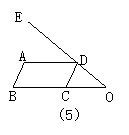
10.如图5,已知AB∥CD,AD∥BC,∠B=60°,∠EDA=50°,则∠CDO=_______.
11.若两条平行线被第三条直线所截,则同旁内角的平分线互相________.
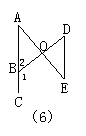
12.如图6,ABC是直线,∠1=150°,∠D=65°,要证AB∥DE,请完善证明过程,并在括号内填上相应依据.∵ABC是直线(已知),∴∠1+∠2=_______°( ),
∵∠1=115°(已知),∴∠2=_______°.∵∠D=65°,∴∠2=∠D( ),
∴AB∥DE( )
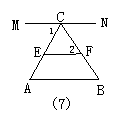
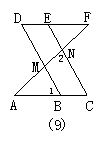
13.如图7,已知∠1=∠A,∠2=∠B,要证MN∥EF,请完善证明过程,并在括号内填上相应依据:∵∠1=∠A(已知),∴_______∥______( ).
∵∠2=∠B(已知),∴______∥________( ),
∴MN∥EF( )
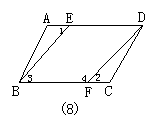
14.如图8,已知AD∥BC,∠1=∠2,要证∠3+∠4=180°,请完善证明过程,并在括号内填上相应依据:∵AD∥BC(已知),∴∠1=∠3( ),
∵∠1=∠2(已知),∴∠2=∠3( ),
∴________∥________( ),
∴∠3+∠4=180°( ).
15. 如图9,已知DF∥AC,∠C=∠D,要证∠AMB=∠2,请完善证明过程,并在括号内填上相应依据:∵DF∥AC(已知),∴∠D=∠1( ),
∵∠C=∠D(已知),∴∠1=∠C( ),
∴DB∥EC( ),
∴∠AMB=∠2( ).
二、选择
16.下列语句中,不能判定两直线平行的是( ).
A.内错角相等,两直线平行 B.同位角相等,两直线平行
C.同旁内角相等,两直线平行 D.同一平面内,垂直于同一直线的两条直线平行
17.如图10,若∠1是它的补角的3倍,∠2等于它的余角,则AB和CD的关系是( )
A.平行 B.相交 C.平行或相交 D.不能确定
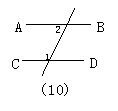
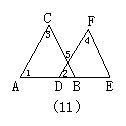
18.如图11,已知∠1=∠2,∠3=∠4,求证:AC∥DF,BC∥EF.证明过程如下:
∵∠1=∠2(已知),∴AC∥DF,(A,同位角相等,两直线平行)
∴∠3=∠5.(B.内错角相等,两直线平行)
又∵∠3=∠4(已知),∴∠5=∠4,(C.等量代换)
∴BC∥EF.(D.内错角相等,两直线平行)
理由填错的是( ).
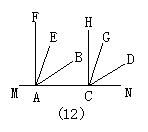
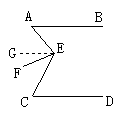
19.如图12,FA⊥MN于A,HC⊥MN于C,指出下列各判断中,错误的是( )
A.由∠CAB=∠NCD,得AB∥CD; B.由∠DCG=∠BAC,得AB∥CD
C.由∠MAE=∠ACF,∠DCG=∠BAE,得AB∥CD; D.由∠MAB=∠ACD,得AB∥CD
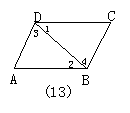
20.如图13,若AB∥CD,则下列结论正确的是( ).
A.∠3=∠4; B.∠A=∠C; C.∠3+∠1+∠4=180°; D.∠3+∠1+∠A=180°
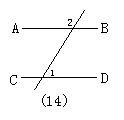
21.如图14,AB∥CD,若∠2是∠1的2倍,则∠2等于( )
A.60° B.120° C.90° D.150°
22.在同一平面内有三条直线,如果要使其中两条且只有两条平行,那么它们( )
A.有三个交点;B.有两个交点;C.只有一个交点;D.没有交点
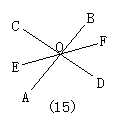
23.写出“对顶角的平分线在一条直线上”的已知、求证,
并画出图形,如图15,已知AB,CD相交于O,OE平分∠AOC,
求证:E,O,F在一条直线上,以上有错误的是( )
A.图形;B.已知;C.求证;D.已知和求证都错.
三、解答.
24.如图,已知∠1=∠2,AB∥CD,求证:CD∥EF.
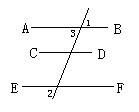
25.如图,已知AB∥CD,∠3=30°,∠1=70°,求∠A-∠2的度数.
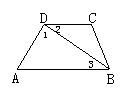
26.如图,已知AB∥CD,∠BAE=40°,∠ECD=70°,EF平分∠AEC,求∠AEF的度数.
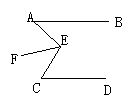
27.如图,已知AB∥CD,∠BAE=30°,∠DCE=60°,EF,EG三等分∠AEC.(1)求∠AEF的度数;(2)求证:EF∥AB.
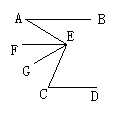
28.如图,已知在△ABC中,EF⊥AB,CD⊥AB,G在AC边上,∠1=∠2,求证:∠AGD=∠ACB.
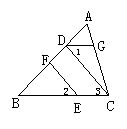
29.如图,已知BD平分∠ABC,∠1=∠2,求证:AB∥CD.
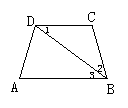
30.如图,已知∠4=∠B,∠1=∠3,求证:AC平分∠BAD.
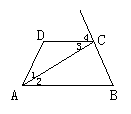
31.如图,已知AB,CD分别垂直EF于B,D,且∠DCF=60°,∠1=30°,求证:BM=AF.
32.证明:垂直于同一直线的两条直线平行.(要求写出已知、求证,作图,并写出证明过程)
答案:
一、1.在同一平面上; 2.两相交和平行; 3.一 4.平行;
5.(1)同位角相等,两直线平行.(2)同旁内角互补,两直线平行.(3)内错角相等,两直线平行.(4)两直线平行,同位角相等.(5)两直线平行,同旁内角互补.(6)两直线平行,内错角相等
6.40° 7.平行 8.47°90° 9.65° 10.70° 11.垂直 12.180平角的性质65°等量代换内错角相等,两直线平行 13.MN AB 内错角相等,两直线平行 EF AB 同位角相等,两直线平行平行于同一直线的两条直线平行
14.两直线平行,内错角相等 等量代换 BE FD 同位角相等,两直线平行 两直线平行,同旁内角互补
15.两直线平行,内错角相等 等量代换 同位角相等,两直线平行两直线平行, 同位角相等
二、16.C 17.A 18.B 19.B 20.D 21.B 22.B 23.B
三、24.证明:∵∠1=∠2,∠1=∠3,
∴∠2=∠3,
∴AB∥EF.
又∵AB∥CD,
∴CD∥EF.
25.∵∠A+∠1+∠3=180°,
∴∠A=180°-∠1-∠3=180°,
又∵AB∥CD,
∴∠2=∠3=30°,
∴∠A-∠2=80°-30°=50°.
26.如答图,过E作EG∥AB,
∴∠A=∠AEG.
又∵∠BAE=40°,
∴∠AEG=40°.
∵AB∥CD,
∴EG∥CD,
∴∠GEC=∠ECD.
∵∠ECD=70°,
∴∠GEC=70°,
∴∠AEC=∠AEG+∠GEC=40°+70°=110°.
又∵EF平分∠AEC,
∴∠AEF=
∠AEC=55°.
27.(1)∠AEF=30°.(2)略.
28-32.(略)