初一数学第一学期第3周综合练习
备课人：袁强辉
修改人：严均亮
教学目标：
1、进一步掌握数轴、相反数、绝对值的相关知识
2、能正确进行数轴、相反数、绝对值的相关运算
3、让学生认识到自己的不足并进行查漏补缺
重难点：
重点：目标2、3
难点：目标3
教学过程：
一、知识回顾和基础练习(35分钟)
问题1： 什么叫数轴？数轴的三要素是什么？出一个数轴来？
解析：每一个有理数都可以用数轴上唯一确定的点来表示。但反过来以后可以看到，数轴上任一点并不一定表示有理数。表示正有理数的点在原点的右边，表示零的点是原点，表示负有理数的点在原点的左边
练习：
1、指出下图中所画的是不是数轴，为什么？
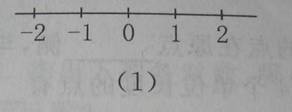
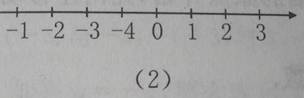
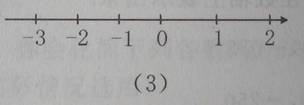
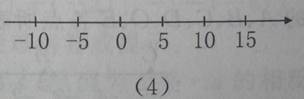
2、请你把下列各数用数轴上的点表示出来
―2、―1、0、5、0.5、－1.5
3、写出下图中数轴上的点A、B、C、D四个点所表示的有理数
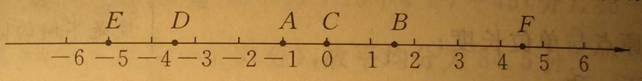
4、从数轴上观察，大于-3小于2的整数有
5、已知一个点到原点的距离为5个单位，则这个点的所表示的数是：
6、文具店、书店和玩具店依次坐落在一条东西走向的大街上，文具店在书店西边30m处，玩具店在书店东边90m处，小明从书店沿街向东走40m，接着又向东走-70m，此时小明在玩具店 边 处
7、下列说法正确的是
A。数轴上的一个点可以表示两个不同的有理数
B。数轴上有两个不同的点表示一个有理数
C。任何一个有理数都可以在数轴上找到与它对应的唯一的点
D。有的有理数不能在数轴上表示出来
8、设a是一个正数，则数轴上表示数a的点在原点的 边，与原点的距离是 个单位长度；表示数－a的点在原点的 边，与原点的距离
是 个单位长度；
问题2：什么叫互为相反数？（互为相反数就是在原点两侧且到原点等距的两点所表示的数。）
相反数的性质？（只有符号不同的两个数是互为相反数，a的相反数为－a；）
各点所表示的数的绝对值是多少？绝对值的几何意义？（在数轴上，表示数a的点到原点的距离叫做数a的绝对值）绝对值的代数意义？(
=a（a＞0），=0（a=0），=－a（a＜0）一个正数的绝对值是它本身；一个负数的绝对值是它的相反数；零的绝对值是零。
9、
（1）―2.3是 的相反数， 的相反数是0.7
（2）
与 互为相反数
（3）若a=13，那么－a=
10、化简下列各数
（1）、－（+3）；（2）、－（－2）；
（3）、+（+4）;（4）、+（－2）；
问题3：数轴上表示两个互为相反数的点和原点有什么关系？两个互为相反数的和是多少？
11、如图所示，表示互为相反数的两个数是（）
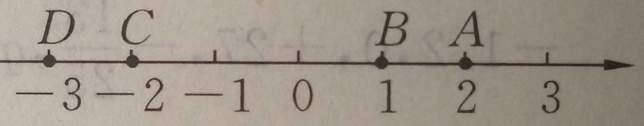
A。点A和点D B。点B和点C
C。点A和点C D。点B和点D
12、下面两个数互为相反数的是（）
A。－（+7）与+（－7）
B。－0.5与－（+0.5）
C。－1.25与
D。＋（－0.01）与－（－
）
问题4：什么叫绝对值？
一般地，数轴上表示数a的点与原点的距离叫做数a的绝对值，记作︱a︱.
13、求下列各数的绝对值
（1）+8
（2）－7.2 （3）0 （4）－5
14、（1）绝对值是5的数有几个？各是什么？
（2）绝对值是0的数有几个？各是什么？
（3）绝对值是－9的数有没有？为什么？
15、判断下列说法是否正确：
（1）符号相反的数互为相反数；
（2）符号相反且绝对值相等的数互为相反数
（3）一个数的绝对值越大，表示它的点在数轴上越靠右
（4）一个数的绝对值越大，表示它的点在数轴上离原点越远
问题5：正数、零、负数的大小比较是怎样？
两个负数怎样比较大小？
16、比较下列各组数的大小
（1）―
与―
（2）―与―
（3）－（－0.3）与
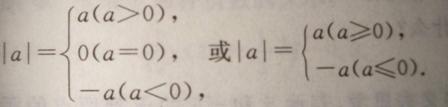
17、
+
=0，求a、b的值
18、分层导学P14第1、4题
二、小结
这节课我们复习有关数轴、相反数、绝对值的相关知识，这三个知识点是互相联系的，我们一定要把这相关的内容联系记忆。
三、小测（8分钟）
1、在数轴上表示下列各数，并用<号进行排列
－5、＋3、―3.5、0、2.5、
、―
2、分别写出－4、＋2.5、―
的相反数
3、写出下列各数的绝对值
－125、＋3.5、0、-
4、化简下列各数
－（－30）、－（＋3）、+（－1.2）、+（+）
5、比较大小
（1）－2.8 0 （2）－
－
（3）－
－3.14 （4）－（－4） －
6、若
=4，则x的值为
四、作业
分层导学
P8第3题，P10知识回顾1、基础联系1，P13
第8、9题