3.1 多姿多彩的图形
A卷 基础知识达标版
（45分钟 100分）
一、选择题
1．以三角形一直角边为轴旋转一周形成（ ）
A．圆柱 B．三棱柱 C．圆锥 D．以上都不对
2．六棱柱展开后，底面一定是（ ）
A．三边形 B．四边形 C．五边形 D．六边形
3．圆柱和圆锥的不同之处在于（ ）
A．底面的形状 B．底面的个数 C．侧面的个数 D．无法确定
4．点滚动后形成（ ）
A．点 B．线 C．面 D．体
5．四棱柱共有（ ）个面．
A．5 B．6 C．7 D．8
6．下面图形经过折叠可以围成一个棱柱的是（ ）
A B C D
7．下列图形中是正方体的展开图的为（ ）
A B C D
8．把图1所示的图形折叠起来围成一个正方体，应该得到的是（ ）
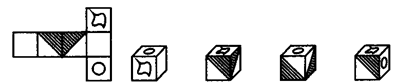
(1) A B C D
二、填空题（每题5分，共35分）
9．长方体有_____个顶点，经过每个顶点有______条边，共有_____条边．
(2) (3) (4)
10．把一个八边形的一个顶点与其余各顶点连接，可把这个八边形分割成______个三角形．
11．图2中的几何体有_____个面，面与面相交成______条线．
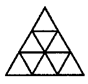
12．数一数图3中共有_____个三角形．
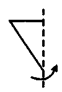
13．如图4所示，图形绕虚线旋转一周得到的立体图形是______．
14．圆柱和棱柱的相同之处在于________．
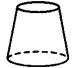
15．一矩形绕其一边旋转形成的几何体是________．
三、解答题（每题11分，共33分）
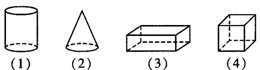
16．将下列几何体分类，并说明你分类的理由．
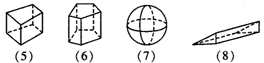
17．写出左视图为三角形的几何体，至少写两种．
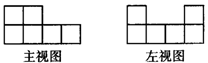
18．用小立方块搭一个几何体，使得它的主视图和左视图如图所示，那么，要摆出这样的几何体最多需要多少个小立方块？最少需要多少个小方立块？
B卷 发散创新应用版
（45分钟 100分）
一、综合题（3题12分，其余各10分，共32分）
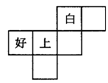
1．如图所示为正方体的平面展开图，现已填上三个字，请你填上所空的三个字，使之与相对的面内的字具有相反意义．
2．从一个六边形的一个顶点出发，分别连接其余各顶点，可以把这个六边形分割成多少个三角形？如果是十边形呢？是二十边形呢？
3．如图所示，请画出圆柱体和圆锥体的三视图．
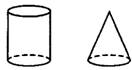
二、应用题（每题10分，共30分）
4．找一找汉字、英文字母中的几何图形，比较一下汉字、英文字母的手写体与印刷体中，谁的几何体图形多？为什么？
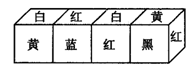
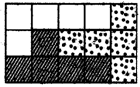
5．在正方体的六个面分别涂上红、黄、蓝、白、黑、绿这六种颜色，现有涂色方式完全相同的四个正方体，如图3-1-8所示，拼成一个长方体，问涂红、黄、白三种颜色的对面分别是哪一种颜色？
6．如图是一个3×5的方格纸，现将其剪为三部分，使每部分可以折成一个没有顶盖的小方盒，问如何剪？
三、创新题（每题15分，共30分）
7．一位父亲有一块正方形的土地，他把其中的
留给自己，其余的平均分给他的四个儿子，如图所示，他想使每个儿子获得的土地面积相等，形状相同，这位父亲应该怎么分？
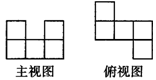
8．用小立方块搭一个几何体，使得它的主视图和俯视图如图所示，这样的几何体有几种？
四、中考题（8分）
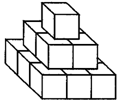
9．一个画家有14个边长为1m的正方体，他在地面上把它们摆成如图所示的形式，然后他把露出的表面都涂上颜色，那么被涂上颜色的总面积是（ ）．
A．19cm2 B．21cm2 C．33cm2 D．34cm2
答案:
A卷
一、
1．C 分析：以三角形一直角边为轴旋转一周为360度，则另一直角边形成一个圆，这样就排除了B．斜边旋转一周则成为一扇形，二者的结合则构成一个圆锥图形，故应选C．
2．D 分析：棱柱体有一个特征：侧棱的个数等于底面多边形的边数，故选D．点拨：抓住侧棱柱与底面边数相等的关系．
3．B 分析：圆柱和圆锥相同之处在于：底面都是圆，一个侧面，且圆柱底面有两个圆，而圆锥为一个圆，故应选B．
4．B 分析：点的滚动变成无数个连续的点，而无数个连续的点则构成一条线，故应选B．
点拨：此题可以根据线的概念直接得出．
5．B 分析：棱锥由一个底面和若干侧面构成，侧面的个数与棱数相同，故应选B．
6．A 分析：图C、图D底面有四条边，侧面有3个，显然与三棱柱、四棱柱的特点不符，故C、D不能围成棱柱．图B的两个底面在侧面同侧，折叠后不能围成棱柱，图A符合棱柱特点，故选A．
7．C 分析：正方体有6个面，每个面都是正方形；有12条棱，所有棱长都相等；有8个顶点，每个顶点都有3条棱通过，4个图均符合以上特点，而A图为9个顶点，有3条棱通过，D图为7个，B图为5个，C图为8个，因C图符合题意，故选C．点拨：找出有三条棱通过的顶点．
8．B 分析：展开图中上下两侧的面折叠后将是相对的两个面，故A项、D项可排除．带有阴影三角形的两个面有一条边重合，折叠后两个阴影三角形仍有一条公用边，故C项也排除．B符合要求，故选B项．
二、
9．8 3 12 分析：长方体有12条棱，8个顶点，且每个顶点都有三条棱通过．
10．6 分析：多边形一个顶点与其他顶点相连接的个数为（n-2）个，故八边形按要求可分为6个三角形．
11．3 2 分析：圆柱体有一个侧面和上下两个底面，侧面和底面各交成一条线，它们都是曲的．
点拨：图中的几何体为主视图．
12．13 分析：三条线段首尾顺次连接构成三角形，线段长短不同，所构成的大小便不同．
13．圆锥 分析：线段上一点水平绕轴旋转一周构成一个圆，而与轴成一角度旋转形成一个曲面，从而具备了圆的特征．
14．都有两个底面 分析：几何体都是点、线、面组成的．圆柱和棱柱都有上下两个底面，这也是两者的相同之处．
15．圆柱 分析：矩形共有四条边，绕其一边旋转会构成两个圆面和一个曲面，这符合圆柱体的特征．
三、
16．若按柱、锥、球划分，可分三类，即（1）（3）（4）（5）（6）（8）是一类，（2）是一类，（7）是一类；若按围成的体的面划分，可分两类，即（1）（2）（7）是一类，（3）（4）（5）（6）（8）是一类． 分析：分类应按某种标准进行合理的分类，不同的标准可以得到不同的答案，因此，本题答案不唯一．
17．圆锥体，四棱锥 分析：从不同的方向观察同一物体时，可能看到不同的图形，其中从左面看到的图叫左视图，由此可得出答案．
18．最多需要20个，最少需要10个 分析：本题应根据主视图和左视图确定小立方块个数的最大值和最小值．如由主视图可知有4列，结合左视图可得每列小立方块个数的最大值分别为6，6，4，4，因此最多需要20个．同理可知每列小立方块个数的最小值分别为6，2，1，1，因此最少需要10个．
B卷
一、1．
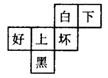
分析：正方体展开图中，每一组相对的面一定是不相邻的两个面，由此可以推出“白”字面一定是最下面的那个面，“上”字面一定是最上面的那个面． 点拨：可以动手做一做．
2．4 8 18 分析：过n边形一个顶点可得到（n-3）条对角线，并且将n边形分成（n-2）个三角形，故六边形，十边形和二十边形分割的三角形个数分别为4，8，18．
3．圆柱的三视图
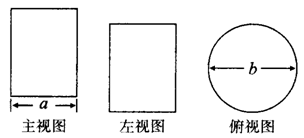
圆锥的三视图
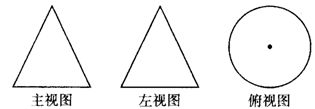
分析：从不同方向看几何体会有不同形状，正面看为正视图，左面看为左视图，从上往下看为俯视图．
二、
4 印刷体的几何图形多 分析：印刷体多采用宋体字，宋体字笔画横平竖直，规范划一，而手写体多向右倾斜，且各人风格多样，所以，印刷体中的几何图形多一些．
5．红色对面是绿色，黄色对面是蓝色，白色对面是黑色．
分析：本题用逆推法．从图中第二个正方体可知，红色的对面不是蓝色，从第三个正方体可知红色对面不是白色，从第四个正方体可知红色对面不是黄色和黑色，因此红色对面是绿色．同样，观察图可知黄色对面不是白、黑、红、绿，因此，黄色对面就是蓝色了，最后就可知白色对面是黑色．
6．
分析：没有顶盖的小方盒共有五个面，其展开图的交点必须有三条棱通过，并且至少有一个点有四条棱通过．
三、7．
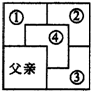
分析：父亲和四个儿子分割一个正方形，父亲留，则所剩三个小正方形每一个再分割为四个小正方形，并且让出一个，土地面积就会相等．所让的三个小正方形必有一条棱重合才能为一体，故如图所分就会形状相同．
8．9种 点拨：第一层有5个方块，第二层有2个方块或3个方块或4个方块三种情况，当第二层有2个方块时，有4种情况；当第二层有3个方块时，有4种情况；当第二层有4个方块时，有1种情况，所以共有9种几何体．
四、
9 分析：露出的总面积=总面积-未露出的总面积．由图可以看出，14个正方体共有84个面，图中未露出的面共有51个，即露出的面有33个，所以露出的总面积为33×1×1=33（cm2）． 解：选C．
点拨：解题关键是数清各种面的个数．