3.4 角的比较与运算
A卷 基础知识达标
（45分钟 100分）
一、选择题（每题5分，共35分）
1．下列语句中，正确的是（ ）．
A．比直角大的角钝角; B．比平角小的角是钝角
C．钝角的平分线把钝角分为两个锐角; D．钝角与锐角的差是锐角
2．两个锐角的和（ ）．
A．必定是锐角; B．必定是钝角;
C．必定是直角; D．可能是锐角，可能是直角，也可能是钝角
3．两个角的和与这两个角的差互补，则这两个角（ ）．
A．一个是锐角，一个是钝角; B．都是钝角;
C．都是直角; D．必有一个是直角
4．下列说法错误的是（ ）．
A．两个互余的角都是锐角; B．一个角的补角大于这个角本身;
C．互为补角的两个角不可能都是锐角; D．互为补角的两个角不可能都是钝角
5．如果两个角互为补角，而其中一个角比另一个角的4倍少30°，那么这两个角是（ ）．
A．42°，138°或40°，130°; B．42°，138°;
C．30°，150°; D．以上答案都不对
6．如果∠A和∠B互为余角，∠A和∠C互为补角，∠B与∠C的和等于120°，那么这三个角分别是（ ）．
A．50°，30°，130°; B．75°，15°，105°;
C．60°，30°，120°; D．70°，20°，110°
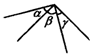
7．如图1所示，∠α+∠β=90°，∠β+∠γ=90°，则（ ）．
A．∠α=β B．∠β=∠γ C．∠α=∠β=∠γ D．∠α=∠γ
(1) (2) (3)
二、填空题（每题5分，共25分）
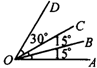
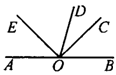
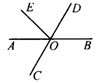
8．如图2，OB是_____的角平分线；OC是_____的角平分线，∠AOD=______，∠BOD=______度．
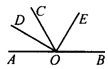
9．如图3，已知OE平分∠AOB，OD平分∠BCO，∠AOB为直角，∠EOD=70°，则∠BOC的度数为_______．
10．∠1=
∠A，∠2=∠A，则∠1和∠2的关系是_______．
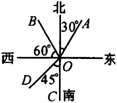
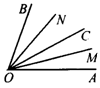
11．如图4，射线OA表示北偏东_____，射线OB表示_____30°，射线OD表示南偏西_______，欲称西南方向，射线OC表示________方向．
(4) (5) (6)
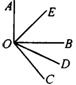
12．如图5，小于平角的角有______个，∠EOC=_____+_______．
三、解答题（每题10分，共40分）
13．如图6所示，直线AB上一点O，任意画射线OC，已知OD、OE分别是∠AOC、∠BOC的角平分线，求∠DOE的度数．
14．如图3-4-5所示，已知∠BOD=2∠AOB，OC是∠BOD的平分线，试表示出图中相等的角．
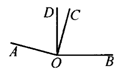
15．如图所示，已知∠AOB=165°，∠AOC=∠BOD=90°，求∠COD．
16．如图所示，直线AB、CD相交于O，OE为射线，试问，图中小于平角的角共有几个？
请一一列出．
B卷 发散创新应用
（45分钟 100分）
一、综合题（1题21分，2题13分，共34分）
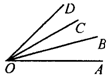
1．（1）如图所示，ON是∠BOC的平分线，OM是∠AOC的平分线，如果∠AOC=28°，∠BOC=42°，那么∠MON是多少度？
（2）如果∠AOB的大小保持与上图相同，而射线OC在∠AOB的内部绕点O转动，那么射线OM、ON的位置是否发生变化？
（3）∠MON的大小是否发生变化？如果不变，请说出其度数，如果变化，请说出变化范围．
2．一个角的补角是它的余角的3倍但少20°，求这个角的大小．
二、应用题（每题14分，共28分）
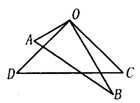
3．有一张地图（如图），有A、B、C三地，但地图被墨迹污损，C地具体位置看不清楚了，但知道C地在A地的北偏东30°，在B地的南偏东45°，你能确定C地的位置吗？
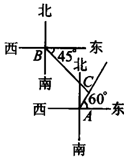
4．如图所示，一只蚂蚁从O点出发，沿北偏东45°的方向爬行2.5cm，碰到障碍物（记作B）后折向北偏西60°的方向爬行3cm（此时位置记作C点）．
（1）画出蚂蚁的爬行路线；（2）求出∠OBC的度数．
三、创新题（每题14分，共28分）
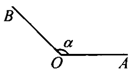
5．如图所示，已知钝角∠α，画出它的补角和它的补角的余角．
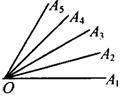
6．如图所示，共有多少个角？一般地，你能得到什么结论？
四、中考题（每题5分，共10分）
7．如图所示，将一副三角板叠放在一起，使直角的顶点重合于点O，则∠AOC+∠DOB的度数为______度．
8．若∠A=34°，则∠A的余角度数为（ ）．
A．54° B．56° C．146° D．66°
答案:
一、
1．C 分析：从锐角、钝角的定义入手，比平角小的角有可能是直角或锐角，比直角大的角可能是平角或周角．设α是钝角，90°<α<180°，45°<
<90°，可见α的一半是锐角．
2．D 点拨：从锐角的定义全面考虑．
3．D 分析：设这两个角的度数分别为x、y，
由两个角互补的定义得（x+y）+（x-y）=180°，2x=180°，则x=90°，故选D．
4．B 分析：当一个角是钝角时，它的补角是锐角，而锐角小于钝角．
5．B 点拨：用验证法，从倍数关系与两角之和应为180°两方面考虑．
6．B 点拨：用验证法得知及是正确答案．
7．D 点拨：∠α和∠γ都是∠β的余角．
二、
8．∠AOC ∠AOD 60° 45
点拨：关键在于正确使用角平分线的定义．
9．50° 分析：∠EOD的度数是∠AOC的度数的一半，而∠BOC=∠AOC-∠AOB．
10．相等 分析：∠1为∠A的一半，∠2为∠A的一半，则∠1=∠2．
11．30° 北偏西 45° 正南
12．9 ∠COD ∠DOE
分析：以OA为角的始边，分别以OE、OD、OC和OB为终边形成∠AOE、∠AOD、∠AOC和∠AOB；以OE为始边，分别以OD、OC和OB为终边所形成的角为∠EOD、∠EOC和∠EOB；以OD为始边分别以OC、OB为终边所形成的角为∠DOC和∠DOB；以OC为始边，OB为终边所形成的角为∠COB．这些角中除∠AOB为平角除外，故共有9个角．因OC为∠DOB内的一条射线，故∠EOC=∠COD+∠DOE．
三、
13．90° 分析：因为OD平分∠AOC，OE平分∠COB，∠DOC=∠AOC，∠COE=∠BOC，∴∠DOE=∠DOC+∠COE=∠AOC+∠BOC=（∠AOC+∠BOC）=∠AOB，
∵∠AOB=180°，∴∠DOE=×180°=90°．
点拨：∠DOE=∠DOC+∠COE，利用角平分线定义，可得∠DOE=∠AOC+∠BOC．
14．∠AOB=∠BOC=∠COD，∠AOC=∠BOD
分析：利用角平分线的定义和题目中提供的倍数关系．
∵∠BOD=2∠AOB．OC是∠BOD的平分线，
∴∠DOC=∠COB=∠AOB．
又∵∠DOC=∠COB=∠AOB，∠DOC+∠BOC=∠BOC+∠AOB，即∠BOD=∠AOC．
点拨：等角的和仍相等．
15．15° 分析：
（1）∠COD是∠BOD与∠BOC之差，
而∠BOC是∠AOB与∠AOC之差．
解：∠BOC=∠AOB-∠AOC=165°-90°=75°，∠COD=∠BOD-∠BOC=90°-75°=15°．
（2）∠AOC+∠BOD=180°①，∠AOB=165°②，①式中的度数大于②式中的度数，
这是因为∠AOC与∠BOD中都含有∠COD，即∠AOC+∠BOD中有两个∠COD，
而在∠AOB中只有一个，所以两者之差即∠COD的度数．
解：∠COD=（∠AOC+∠BOD）-∠AOB=（90°+90°）-165°=15°．
16．8个，它们是∠AOE、∠AOD、∠EOD、∠EOB、∠DOB、∠BOC、∠COA、∠COE．
分析：当构成角的两边的射边方向相反时，所夹的角称为平称．
此题要求列出小于平角的角，只要从点O发出的五条射线中任取两条，除去OA与OB、OC与OD两组即可．
B卷
一、（1）35° 分析：∠MON=∠MOC+∠CON，根据角平分线的定义
∠MOC=∠AOC=×28°，∠CON=∠COB=×42°，从而∠MON的度数可求．
解：∠MON=∠MOC+∠CON=∠AOC+∠COB=（∠AOC+∠COB）
=（28°+42°）=35°．
（2）OM、ON的位置发生变化
分析：当OC绕点O转动时，∠AOC的大小发生变化，
由于∠AOM=∠AOC，所以∠AOM的度数也发生变化，
又因为射线OA的位置不变，
所以OM的位置随OC的位置变化而变化．
（3）∠MON的大小不变，为∠AOB=35°．
分析：∠MON=∠AOC+∠BOC=（∠AOC+∠BOC）=∠AOB=×70°=35°．
2．这个角为35°
分析：设这个角为α，则它的补角为180°-α，它的余角为90°-α，
依题意知180°-α=3（90°-α）-20°，解得α=35°，即这个角为35°．
二、
3.
分析：因C在A地北偏东30°，在B地南偏东45°，在A、B两点作出方位图C，既在AC上，又在BC上，所以求出两条射线的交点即可．
4．（1）
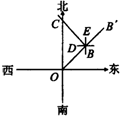
分析：先以O为顶点，表示正北方向的射线为角的一边，画45°的角，使它的一边OB′落在东与北之间，在射线OB′上取OB等于2.5cm，同理可以B点为顶点，画出BC=3cm，则：OB、BC是蚂蚁所行的路线．
（2）75°
分析：∵∠COB=∠OBD=45°，∠EBC=60°，∠DBC=90°-∠EBC=90°-60°=30°，
那么∠OBC=∠OBD+∠DBC=45°+30°=75°．
三、
5．
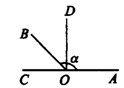
如图，∠BOC是∠α的补角，∠BOD即是它们的补角的余角．
分析：延长AO，则∠BOC即是∠α的补角，
∵∠BOC+∠α=180°；过O作OD⊥CA，
则∠BOD即是它的补角（即∠BOC）的余角，
∵∠BOD+∠COB=90°．
6．10个角 
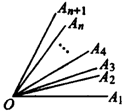
个角
分析：如图以OA1为始边的角有：∠A1OA2，∠A1OA3，…∠A1OAn+1，共n个，
同理以OA2为始边的角有（n-1）个，…以OAn为始边的角只有∠AnOAn+1，
所以共有n+（n-1）+…+1=个角．…
四、
7 分析：观察图形可知，所求两角之和刚好是两个直角的和．
解：∠AOC+∠DOB=2×90°=180°．
点拨：结合图形解题是几何的一大特点．
8．分析：如果两个角的和等于90°，则这两个角互余．90°-34°=56°．
解：选B．点拨：根据余角的定义计算．