七年级数学第三次月考试卷
七年级数学 得分
一．选择题
| 题号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 答案 |
|
|
|
|
|
|
|
|
|
|
|
|
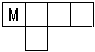
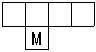
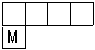
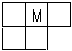
1、如图，有一个无盖的正方体纸盒，下底面标有字母“M”,沿图中粗线将其剪开展成平面图形，想一想，这个平面图形是
(A) (B)
 |  | ||
(C) (D)
2、将一张长方形纸如图所示对折三次，则产生的折痕与折痕间的位置关系有
A、平行 B、垂直 C、平行或垂直 D、无法确定
3、把一张边长为24cm的正方形纸片的四个角上各剪去一个同样大小的正方形后，制成一个无盖的长方体，要使所制长方体容积最大，剪去的正方形的边长应为
A．1cm B．2cm C．3cm D．4cm
4、利用一副三角板上已知度数的角，不能画出的角是
A、15° B、135° C、165° D、100°
5.在时刻8：30，时钟上时针和分针的夹角为
A、85° B、75° C、70° D60°
6.下列说法错误的是
A、在同一平面内，过一点有且只有一条直线与已知直线垂直.
B、过一点有且只有一条直线与已知直线平行.
C、二条直线相交有且只有一个交点. D、若二条直线相交所形成的四个角相等,则这二条直线互相垂直.
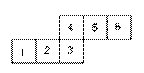
0. 如图是正方体的平面展开图，每个面都标注了数字，如果5在正方体的右面，4在下面，那么后面的数字是
A. 1 B. 4 C. 5 D. 6
 | |||
 | |||
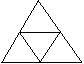8、如图，四个三角形均为等边三角形，将图形折叠得到的立体图形是
A六面体 B三棱锥 C三棱柱 D四棱锥
9．设“●、■、▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架也平衡，那么“？”处应放“■”的个数为
 |  |
（1） （2） （3）
A.5 B.4 C.3 D.2
10．两年期定期储蓄的年利率为2.25％，按照国家规定，所得利息要缴纳20％的利息税，王大爷于2002年6月存入银行一笔钱，两年到期时，共得税后利息540元，则王大爷2002年6月的存款额为 元
A．20000 B.18000 C.15000 D.12800
11．如图是一块带有圆形空洞和方形空洞的小木板，则下列物体
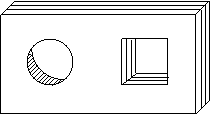中既可以堵住圆形空洞，又可以堵住方形空洞的是
 |
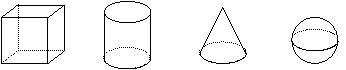A B C D
12．当１＋(3m－5) 2 取最小值时，关于x的一元一次方程
解是
A .
B. 
C.
D.－
二．填空
13.．已知(m-2)xm2-3+(m+2)+2=0是关于x的一元一次方程,则m=
14.已知:∠1和∠2互余,且∠1=27°36′则∠2= °
15.如图,将一副三角板叠放在一起,使直角顶点重合于点o,则∠AOC+ ∠DOB的度数为
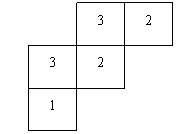
16.如图:两个图形是有几个相同的小长方体堆成的物体的年视图,那么堆成的小长方体最多 个,最少 个.
17.已知一个棱住有2n个顶点,则该棱住有 个侧面, 条棱.
18．甲从o点向北偏东60°走了200米,到达A处,乙从o点向北偏西60°走了200米, 到达B处, 则B在A的 方向.
19. .已知关于x的方程
的解是－１，则k=
20. 已知点B在线段AC上，AB=8cm，AC=18cm，P、Q分别是AB、AC中点，则PQ=＿＿＿
21．.若(2x+3y)2+︱4x+5y︱=0,则4x+4y+1=
22．一个正五边形与一个正方形的边长正好相等，在它们相接的地方，形成一个完整的“苹果”图案(如图)．如果让正方形沿着正五边形的四周滚动，并且始终保持正方形和正五边形有两条边邻接，那么正方形要绕五边形______圈，才能第一次恢复“苹果”的图形．
三．解答题
23.解方程
(1)
(2)
24 “*”是规定的一种运算法则:a*b=a2－b.
①求5*（-1）的值；
②若3*x=2,求x的值；
③若（－4）*x=2－x, 求x的值.
25.如图，是由小立方块搭成几何体的俯视图，上面的数字表示，该位置小立方块的格数画出主视图 左视图
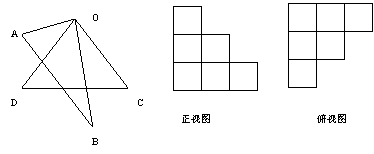
26.如图,C是线段AB的中点,D是线段BC的中点,已知图中所有的线段之和为39,求线段BC的长
27.如图，∠AOB与∠AOD的度数的比为2：11，∠AOB=∠BOD=90°,∠AOB, ∠ BOC的度数。
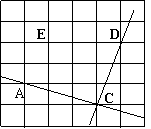
28. 如图，在方格纸中，直线AC与CD相交于点C.
（1） 过点E画直线EF，使EF⊥AC；(2)分别表示（1）中三条直线之间的位置关系；
（2） 根据你观察到的EF与CD间的位置关系，用一句话来解释你的结论.
 |
29.公司需在一个月（31天）内完成新建办公楼的装修工程。如果甲、乙两个工程队合作，12天完成，如果甲单独做8天，剩下的工作由乙独做18天可以完成。
（1）求甲、乙两个工程队单独完成工作的天数；
（2）如果请甲工程队施工，公司每日需付费用2000元，如果请乙工程队施工，公司每日需付费用1400元，在规定的时间内：A、请甲工程队单独完成此项工程；B、请乙工程队单独完成此项工程；C、请甲、乙两个工程队合作完成此项工程，试问：以哪一种方案花钱最少？
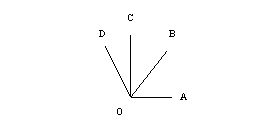
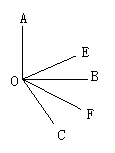
30 如图，已知∠AOB是直角，∠BOC＝600, OE平分∠AOC，OF平分∠BOC.
（1） 求∠EOF的度数；(2)若∠AOC＝ x0，∠EOF＝y0.则请用x的代数式来表示y.
（2） 如果∠AOC+∠EOF＝1560.则∠EOF是多少度？
31、（9分）某商场规定营业员的工资包括基本工资和营业工资两个部分，其中基本工资为500元/月，销售工资是按营业员当月的营业总额的千分之五来计算的。营业员甲为测算自己的营业工资，自己记录了11月份连续七天的营业情况，以2000元为标准，超过的记正数，不足的记负数，记录如下：400、300、-100、200、-300、500、-300；又根据国家税法规定，每月个人所得超过800元的部分为应纳税所得额，需缴纳一定的个人所得税。上缴个人所得税是按下表累加计算的。
| 应纳税所得额 | 税率 |
| 不超过500元的部分 | 5% |
| 超过500元至2000元的部分 | 8% |
| 超过2000元至5000元的部分 | 10% |
| … | … |
请你帮助营业员甲测算出11月份的工资。
该商场营业员乙到银行取工资时发现他10月份的工资比测算的工资少了89元，他先愣了一下，又知道是由于上缴了个人所得税，聪明的同学们，你能求出营业员乙10月份的工资吗？（
该商场经理出台一奖励办法，办法规定：若月营业总额不超过6万元的按原来规定计算当月营业工资，若月营业总额超过6万元但不超过10万元，则超过6万元的部分另加千分之二来计算当月营业工资，若月营业总额超过10万元，则其中的10万元按上面的两个规定，超过10万元的部分另加千分之五来计算当月的营业工资，出台了这一奖励办法之后的某个月营业员丙上缴个人所得税51.4元，那么他这个月的营业总额为__________万元。（不须写出求解的过程）。