七年级下学期阶段性测试数学试卷
（考试时间：90分钟 满分：150分）
一、选择题（每小题4分，共40分）
1、点P（-１，５）所在的象限是 （ ）
Ａ、第一象限 Ｂ、第二象限 Ｃ、第三象限 Ｄ、第四象限
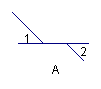
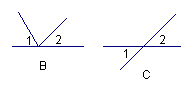
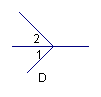2．在下图中，∠1,∠2是对顶角的图形是
（ ）
 |  | ||
3、以下列长度为边的三条线段能组成三角形的是 （ ）
A、2，3，5 B、4，4，9 C、3，5，10 D、5，12，13
4、下列命题为真命题的是 （ ）
A.内错角相等
B.点到直线的距离即为点到直线的垂线段
C.如果∠A+∠B+∠C=180°，那么∠A、∠B、∠C互补
D.同一平面内，垂直于同一直线的两直线平行。
5、如图，由AB∥CD，能推出正确结论的是 ( )
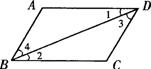A、∠1=∠2
B、∠3=∠4
C、∠A=∠C
D、AD∥BC
（第5题图）
6、已知y轴上点P到x轴的距离为3，则点P坐标为 （ ）
（A）（0，3） （B）（3，0）
（C）（0，3）或（0，–3） （D）（3，0）或（–3，0）
7、一个多边形的内角和等于它的外角和，这个多边形是 （ ）
Ａ、三角形 Ｂ、四边形 Ｃ、五边形 Ｄ、六边形
8、将点A(-1，2)向右平移3个单位长度，再向下平移5个单位长度，则平移后点的坐标是 ( )
A、(2，-3) B、(-2，-3) C、(2，3) D、(-2，3)
9、用同一种下列形状的图形地砖不能进行平面镶嵌的是 （ ）
A.正三角形 B.长方形 C.正八边形 D.正六边形
10、一个三角形有两条边相等，如果这个三角形有两边的长分别为2和7，则它的周长是（ ）
A、9 B、11 C、16 D、11或16
二、填空题（每小题4分，共40分）
11. 剧院里5排2号可以用（5，2）表示，则7排4号用 表示.
12、一个多边形的内角和等于1440°，则这个多边形是 边形
13.如果两个角是对顶角，且互补，则这两个角都是 角。
14.若直线a⊥b,a∥c,则 c___b.
15.点A的坐标为(3，-4),它表示点A在第____象限,它到x轴的距离为_____.
16、把命题“等角的补角相等”改写成“如果…，那么…”的形式是：
___________________________________________________________________
17.在△ABC中,∠A:∠B:∠C=2:3:4,则∠B=______.
18. 一个三角形有两条边相等，其周长为24cm，三角形的一边长为6cm，其他两边长分别为__________________。
19、若点A（a－2，a + 2）在X轴上，则A点坐标为 .
20、某公园用n个正方形和m个正三角形地板砖对一块场地进行平面镶嵌，为了尽可能地减少浪费，又能铺好地面，在确定地板砖购买数量时， n和m之间应满足的关系为 ______ .
三、解答题(共70分)(解答要求写出文字说明, 证明过程或计算步骤, 如果你觉得有的题目有点困难, 那么把自己能写出的解答写出一部分也可以, 可不要有题目下面是空白的喔!)
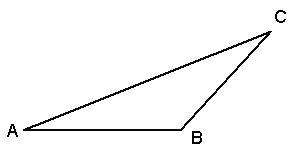
21、（6分）如图，在△ABC中，分别画出：
（1）AB上的高CD；
（2）∠ABC的角平分线BE；
（3）BC上的中线AF。
22. （8分）如图，EF∥AD,∠1=∠2,∠BAC=70°.将求∠AGD的过程填写完整.
解: 因为EF∥AD,
所以∠2=_______(____________________________)
又因为∠1=∠2
所以∠1=∠3(________________________)
所以AB∥________(_____________________________)
所以∠BAC+________=180°(___________________________)
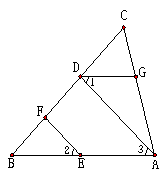因为∠BAC=70°
所以∠AGD=_______
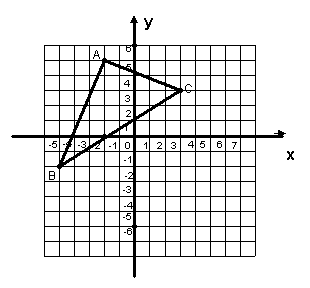23. （8分）将三角形ABC向右平移4单位长度，再向下平移5单位长度，在图上画出对应的三角形A1B1C1，并写出点A1、B1、C1的坐标。
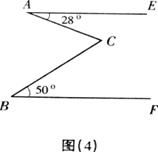
24、(8分)已知：如图(4)，直线AE∥BF，∠EAC=28°，∠FBC=50°，求
∠ACB的度数。
25. （8分）中国象棋中的马颇有骑士风度，自古有“马踏八方”之说，如图六(1)，按中国象棋中“马”的行棋规则，图中的马下一步有A、B、C、D、E、F、G、H八种不同选择，它的走法就象一步从“日”字形长方形的对角线的一个端点到另一个端点，不能多也不能少。
要将图六(2)中的马走到指定的位置P处，即从（四，6）走到(六，4)，现提供一种走法：
(四，6)→(六，5)→(四，4)→(五，2)→(六，4)
(1) 
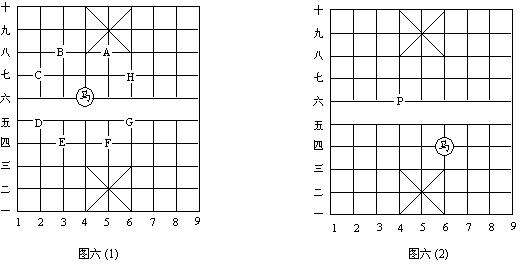下面是提供的另一走法，请你填上其中所缺的一步：
(四，6)→(五，8)→(七，7)→___________________→(六，4)
(2)请你再给出另一种走法(只要与前面的走法不完全相同即可，步数不限)，你的走法是______________________________________________________________
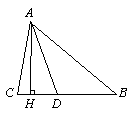
26、（10分）如图，在△ABC中，∠C>∠B，AH⊥CB于H，AD平分∠CAB.
①如果∠B = 40º，∠HAD = 20º，求∠C的度数
②求证：∠HAD =
（∠C-∠B）
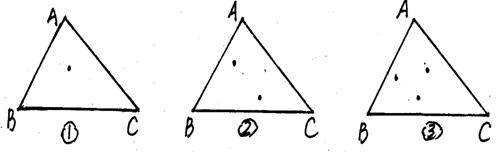
27. （10分） △ABC内分别有1个点，2个点，3个点，……，连同三角形的三个顶点，没有三点在同一直线上，试通过画图探究这些点可以把三角形分割成几个互不重叠的小三角形：
|
（1）图①中，当△ABC内只有1个点时，可分割成 个互不重叠的小三角形。
（2）图②中，当△ABC内只有2个点时，可分割成 个互不重叠的小三角形。
（3）图③中，当△ABC内只有3个点时，可分割成 个互不重叠的小三角形。
（4）根据以上规律，请猜测当△ABC内有n（n为正整数）个点时，可以把△ABC分割成 个互不重叠的三角形。
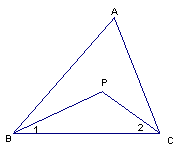28、（10分）如图，P是△ABC内一点，连结PB、PC
（1）当∠1= 
∠ABC，∠2= ∠ACB时你能说明∠P=90°+∠A成立吗？
（2）当∠1=
∠ABC；∠2= ∠ACB时，猜猜看：∠P与∠A又是什么关系？请说明理由。
（3）当∠1=
∠ABC，∠2= ∠ACB时，再猜猜，∠P与∠A又是什么关系？请直接写出∠P与∠A的关系式是：
。
祝贺你已圆满完成本卷！请你认真复查，不要留下遗憾！
参考答案
一、 选一选（13×2分=26分）
1～5 BCDDB 6～10 CBACC
二、填一填（11×3分=33分）
11. (7,4) 12.十 13. 直 14.⊥ 15.四 ,4
16.如果两个角相等,那么这两个角的补角也相等 17. 60°
18. 9cm,9cm 19.(-4,0) 20. 3n+2m=12
三、解答题
21．画图略
22.∠3 两直线平行同位角相等 等量代换
DG 内错角相等两直线平行 ∠AGD 两直线平行同旁内角互补 110°
23. 画图略 A1（2，0） B1（-1，-7） C1（7，-2）
24、因为延长BC交AE于E因为AE∥BF,所以∠B＝∠E=50°
所以∠ACB=∠A+∠E=50°+28°=78°
25. (1)、(五，6)或(八，5) （只需写出其中一个）
(2)、答案有多种，例 (四，6)→(二，5)→(三，3)→(四，5)→(六，4)等
注：正确写出一种给6分，正确写出两种或多于两种，另奖励5分。
26.(1)解成立∠1+∠2=(180 °-∠A)/2=90°-∠A/2
∠P=180°-(90°-∠A/2)= 90°+∠A/2
(2)因为∠1= ∠ABC；∠2= ∠ACB 所以∠1+∠2=（180°-∠A)/3
=60°-∠A/3 所以∠P=180°-(60°-∠A/3)= 120°+∠A/3
（3）∠P=180°-(180°/n-∠A/n)= 180°-180°/n+∠A/n
27.图如下：
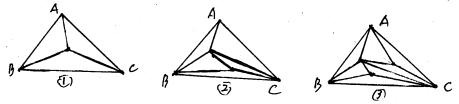
（1）3 （2）5 （3）7 （4）(2n+1)；
28.(1)解成立∠1+∠2=(180 °-∠A)/2=90°-∠A/2
∠P=180°-(90°-∠A/2)= 90°+∠A/2
(2)因为∠1= ∠ABC；∠2= ∠ACB 所以∠1+∠2=（180°-∠A)/3
=60°-∠A/3 所以∠P=180°-(60°-∠A/3)= 120°+∠A/3
（3）∠P=180°-(180°/n-∠A/n)= 180°-180°/n+∠A/n