全等三角形（一）
1.下列关于两个三角形全等的说法不正确的是（ ）
（A）对应边与对应角一定相等；
（B）非对应边与非对应角一定不相等；
（C）周长一定相等；
（D）面积一定相等.
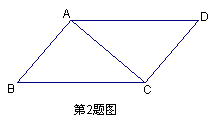
2.如图，若△ABC≌△CDA，∠BAC=∠DCA，∠B=∠D，对于以下结论：
①AB与CD是对应边；②AC与CA是对应边；③点A与点A是对应顶点；④点C与点C是对应顶点；⑤∠ACB与∠CAD是对应角．其中正确的有（ ）
（A）2个 （B）3个 （C）4个 （D）5个
3.如图，把图形沿AC对折，点B与点D重合，则图中全等的三角形有 对，它们是 ．
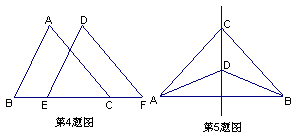
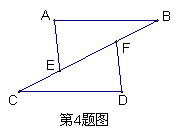4.如图，若△ABE与△DCF全等，A与D，B与C是对应顶点，那么BE的对应边是
，∠AEB的对应角是 ．
5. 根据上题，若∠A=80°，∠B=30°，则
∠CFD= °．
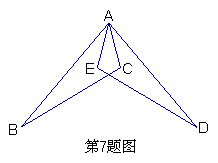
7.如图，△ABC≌△ADE，∠E和∠C是对应角，AB与AD是对应边，写出另外两组对应边和对应角．
 |
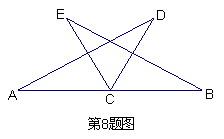
8.如图，点C是AB中点，△ACD≌△BCE，
且AD≠CE．
（1）写出△ACD与△BCE中相等的边与相等的角；
（2）∠ACE与∠BCD相等吗？请说明理由．
 |
全等三角形（二）
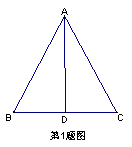
1.如图，下列条件能判定△ABD≌△ACD的有（ ）
①BD=CD，AD⊥BC.
②∠B=∠C，AD平分∠BAC.
③AB=AC，∠BAD=∠CAD.
④BD=CD，∠BAD=∠CAD.
（A） ①② （B）①②③
（C）①②③④ （D）①③
2. 如图，若△ABC≌△DCB，则下列结论中：①∠ECB=∠EBC；②AE=DE；③BE=DE；④△ABE≌△DCE.正确的有（ ）
（A）1个（B）2个（C）3个（D）4个
3.请各举一个三角形稳定性和四边形不稳定的例子：① ；② ．
4. 如图，已知∠ABC＝∠DEF，AB＝DE，要说明△ABC≌△DEF，
（1）若以“SAS”为依据，还须添加的一个条件为 ；
（2）若以“ASA”为依据，还须添加的一个条件为 ；
（3）若以“AAS”为依据，还须添加的一个条件为 ．
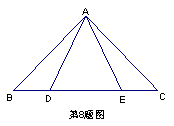
5.如图，CD是线段AB的垂直平分线上，则∠CAD=∠CBD.请说明理由（填空）：
解：∵CD是线段AB的垂直平分线（ ）
∴AC= ， =BD
（ ）
在 和 中，
=BC，
AD= ，
CD= （ ）.
∴ ≌ （ ）
∴∠CAD=∠CBD（ ）.
7. 以下关于三角形全等的结论中：①有三个角对应相等的两个三角形全等；②有三条边对应相等的两个三角形全等；③周长相等的两个三角形全等；④面积相等的两个三角形全等．哪些是正确的？哪些是不正确的？请举例说明．
8.如图，已知AB=AC，AD=AE，BD=CE，
则△ABE≌△ACD，请说明理由．小明同学是这样做的：
解：在△ABE和△ACD中，
AB=AC（已知），
AD=AE（已知），
BD=CE（已知），
∴△ABE≌△ACD（SSS）.
你认为小明的解答是否正确？如果正确，请根据已知条件再改编一个题目并解答；如果不正确，请写出正确的说理过程．
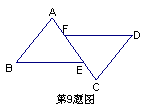
9. 如图，AB=CD,AF=CE，∠A=∠C，那么BE与DF相等吗？请说明理由．
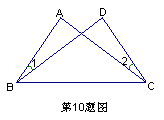
10. 如图，已知∠1＝∠2，∠ABC＝∠DCB．请说明AB＝DC的理由．
11. 如图，A、B两点是湖两岸上的两点，为测A、B两点距离，由于不能直接测量，请你设计一种方案，测出A、B两点的距离，并说明你方案的可行性．
