七年级数学第七章《三角形》水平测试
一、精心选一选（每题2分，共10分）
1．下列说法中错误的是（ ）
A.三角形三条角平分线都在三角形的内部 B.三角形的三条中线都在三角形的内部
C.三角形的三条高都在三角形的内部 D.三角形三条高至少有一条在三角形的内部
2．能把一个三角形分成两个面积相等的三角形是（ ）
A.中线 B.高 C.角平分线 D.以上都不是
3．等腰三角形的两边分别长7cm和13cm，则它的周长是（ ）
A.27cm B.33cm C.27cm或33cm D.以上结论都不对
4．△ABC中，∠A=2∠B＝3∠C，则这个三角形是（ ）
A.锐角三角形 B.直角三角形 C.钝角三角形 D.含30°角的直角三角形
5．下列说法中正确的是 （ ）
A．三角形的外角中至少有两个锐角 B．三角形的外角中至少有两个钝角
C．三角形的内角中至少有一个直角 D．三角形的内角中至少有一个钝角
6． 一个多边形的边数每增加一条，这个多边形的（ ）
A.内角和增加360° B.外角和增加360° C.对角线增加一条 D.内角和增加180°
7.一个多边形只有27条对角线，则这个多边形的边数为（ ）
（A）8（B）9（C）10（D）11
8．下列正多边形中，与正三角形同时使用，能进行镶嵌的是（ ）
Ａ．正十二边形 Ｂ．正十边形 Ｃ．正八边形 Ｄ．正五边形
9．△ABC中，
cm，
cm， c＝14cm,则x的取值范围是 （ ）
A.
B.
C.
D.
10．锐角三角形的三个内角是∠A、∠B、∠C，如果
，
，
，那么
、
、
这三个角中
（ ）
A．没有锐角 B．有1个锐角 C．有2个锐角 D．有3个锐角
二、细心填一填（每题3分，共15分）
1．如图所示，图中的∠1＝______________º．
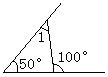
2．如果三条线段a、b、c，可组成三角形，且a=3，b=5，c是偶数，则c的值为 ．
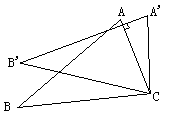
3．如图，将△ABC绕着点C按顺时针方向旋转20°，B点落在
位置，A点落在
位置，若AC⊥
，则∠BAC的度数是__________
4．如果一个多边形的每一个外角都小于45º这样的多边形边数的最小值是_______.
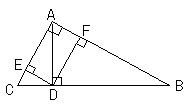
5．如图，在直角三角形ABC中，AC≠AB，AD是斜边上的高，DE⊥AC，DF⊥AB，垂足分别为E、F，则图中与∠C（∠C除外）相等的角有________个。
6．一个直角三角形两锐角的平分线所夹的钝角为 ．
7．一个多边形的每一个外角都等于36
，则该多边形的内角和等于
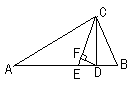
8．如图，△ABC中，∠A = 40°，∠B = 72°，CE平分∠ACB，CD⊥AB于D，DF⊥CE，则∠CDF =_________度。
9.去年11页9题
10.去年11页8题
三、耐心解一解
1．如图，一块模板中AB、CD的延长线相交成80°角，因交点不在板上，不便测量，工人师傅连结AC，测得∠BAC=34°∠DCA=65°，此时，AB、CD的延长线相交成的角是否符合规定？为什么？
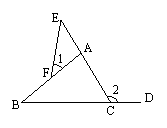
2.如图，在△ABC中，D在BC的延长线上，E在CA的延长线上，F在AB上，试比较∠1与∠2的大小.
3．两个正多边形的边数之比为1∶2，内角和之比为3∶8，求这两个多边形的边数、内角和.
4．在△ABC中AB=AC，AC上的中线BD把三角形的周长分为24cm和30cm的两个部分，求三角形的三边长。
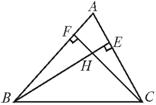
5．在△ABC中，已知∠ABC=66°，∠ACB=54°，BE是AC上的高，CF是AB上的高，H是BE和CF的交点，求∠ABE、∠ACF和∠BHC的度数.
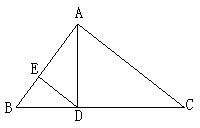
6．如图，在△ABC中，∠BAC=90°，∠B=56°，AD⊥BC，DE∥CA．求∠ADE的度数．
一、
1．C 2．A 3．C 4．D 5．B 6．D 7. B 8．A 9．A 10．A
二、
1．50° 2．4，6 3．70° 4.9 5．3 6．135 7．1440 8．52
9.12 10. 120°
三、
1．不符合规定.理由：因为∠BAC、∠ACD与该角组成一个三角形，根据三角形内角和可知这三个角度之和为180°，所以可以求出这个角的度数为81°，故相交所成的角不符合规定.
2.因为∠2是△ABC的外角，所以∠2>∠BAC（三角形的外角大于和它不相连的内角）.
同理可说明∠BAC>∠1，从而推出∠2>∠1.
3.这两个正多边形分别是五边形和十边形，内角和分别为540°和1440°.（提示：设这两个正多边形的边数分别为n和2n条，根据多边形的内角和公式，可得两正多边形的内角和分别为
和
，由于两正多边形内角和的度数之比为3∶8，所以
）
4．三角形的三边长分别是16cm、16cm、22cm或20cm、20cm、14cm.（提示：设AD＝xcm，BC＝ycm，则CD＝xcm，AB＝2xcm。由题意可得
或
解得
或
）
5．∠ABE＝30°,∠ACF＝30°，∠BHC＝120°.（提示：因为∠ABC=66°，∠ACB＝54°，所以∠A＝60°.因为CE是AC上的高，所以在△ABE中，∠ABE＝180°－∠AEB－∠A＝30°,同理可求得∠ACF＝30°.在四边形AFHE中，∠A＝60°，∠AFH＝∠AEH＝90°，所以∠EHF＝120°）
6．∠ADE＝56°.（提示：因为∠BAC=90°，DE∥AC（已知），所以∠DEA＝180°－∠BAC＝90°.因为AD⊥BC，∠B＝56°，所以BAD＝34°.在△ADE中，因为DE⊥AB，所以∠ADE＝56°.）