平面直角坐标系小结与复习 习题精选（一）
一、选择题
1.已知点A（－3，0），则A点在 （ ）
A.x轴的正半轴上 B.x轴的负半轴上 C.y轴的正半轴上 D.y轴的负半轴上。
2.已知点B（0，－5）则B点在（ ）
A.x轴的正半轴上 B.x轴的负半轴上 C.y轴的正半轴上 D.y轴的负半轴上。
3.已知点P（4，－3），则点P到x轴的距离为（ ）。
A.4 B.－4 C.3 D.－3
4.已知点P（2，－5），则点P到两坐标轴的距离之和为（ ）。
A.2 B.5 C.3 D.7
5.已知点A（x，y），且xy=0，则点A在 （ ）。
A.原点 B.x轴上 C.y轴上 D.x轴或y轴上。
6.已知点P（x，y），且
，则点B在 （ ）。
A.原点 B.x轴的正半轴或负半轴
C.y轴的正半轴或负半轴上 D.在坐标轴上，但不在原点。
7.已知点A（－3，2m－1）在x轴上，点B（n＋1，4）在y轴上，则点C（m，n）在 （ ）
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.已知点A（a，b），则过A且与y轴平行的直线上的点（ ）
A.横坐标是a B.纵坐标是a C.横坐标是b D.纵坐标是b
9.若点B到x轴.y轴的距离分别为8和7，则点B的坐标为（ ）
A.（8，7）、（－8，－7）、（7，8）、（－7，－8）
B.（7，8）、（7，－8）、（－7，8）、（－7，－8）
C.（8，7）、（－8，7）、（－8，－7）、（8，－7）
D.（－7，8）、（7，－8）、（8，－7）、（－8，7）
10.如果点B（x－1，x＋3）在y轴上，那么x= （ ）
A.1 B.－1 C.3 D.－3
11.如果
，那么点N（a，b）关于原点对称的点N′的坐标为（ ）
A.（3，5） B.（－3，－5） C.（－3，5） D.（5，－3）
12.已知点M（3，－2）与点M′（x，y）在同一条平行于x轴的直线上，且M′到y轴的距离等于4，那么点M′的坐标是（ ）
A.（4，2）或（－4，2）
B.（4，－2）或（－4，－2）
C.（4，－2）或（－5，－2）
D.（4，－2）或（－1，－2）
二、填空题
13.若点P在第二象限，且点P到x轴.y轴的距离分别为4，3，那么点P的坐标为______。
14.若点M（a＋5，a－2）在y轴上，则a_______。
15.点P（a＋5，a－2），到x轴的距离为3，则a_______。
16.已知点P（x，y）满足
，则点P的位置是______。
17.若点P（a，b）在第四象限，则点M（b－a，a－b）在_______。
三、解答题
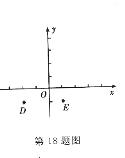
18.设点M（a，b）为的平面直角坐标系中的点，
（1）当a＞0，b＜0时，点M位于第几象限？
（2）当ab＞0时，点M位于第几象限？
（3）当a为任意实数，且b＜0时，点M位于第几象限？
19.在平面直角坐标系中，将坐标为A（2，3），B（4，7），C（6，7），D（4，3）的点用线段依次连接起来形成一个图形。
（1）这四个点的纵坐标保持不变，横坐标变为原来的
，将所得的四个点用线段依次连接起来，所得图形与原图形相比有什么变化？
（2）纵坐标保持不变，横坐标分别加3呢？
（3）横坐标保持不变，总坐标分别加3呢？
（4）横坐标保持不变，总坐标分别乘－1呢？
（5）横，纵坐标分别变成原来的2倍呢？
答案
一、选择题
1.B 2.D 3.C 4.D 5.D 6.A 7.D 8.A 9.B 10.A 11.C 12.B
二、填空题
13.（－3，4） 14. －5 15. －1或5 16.在坐标轴夹角的平分线上 17.第二象限；
三、解答题
18.解：（1）∵a＞0，b＜0，∴点M位于第四象限。
（2）∵ab＞0，∴a＞0，b＞0或a＜0，b＜0。
∴点M在x轴下方，即点M在第三象限或第四象限或在y轴的负半轴上。
（不要漏掉了点M在y轴的负半轴上这一情形）。
19.解：顺次连接ABCD得到一个平行四边形。
（1）这平行四边形与x轴平行的边是原平行四边形的一半。
（2）原平行四边形向右平移3个单位。
（3）原平行四边形向上平移3个点位。
（4）所得平行四边形与原平行四边关于原点对称。
（5）所得平行四边形的各边是原平行四边形的两倍。