5.2.1 平行线同步练习题
一、选择题:(每小题3分,共15分)
1.在同一平面内,两条不重合直线的位置关系可能是( )毛
A.平行或相交 B.垂直或相交; C.垂直或平行 D.平行、垂直或相交
2.下列说法正确的是( )
A.经过一点有一条直线与已知直线平行
B.经过一点有无数条直线与已知直线平行
C.经过一点有且只有一条直线与已知直线平行
D.经过直线外一点有且只有一条直线与已知直线平行
3.在同一平面内有三条直线,若其中有两条且只有两条直线平行,则它们交点的个数为( )
A.0个 B.1个 C.2个 D.3个
4.下列说法正确的有( )
①不相交的两条直线是平行线;②在同一平面内,两条直线的位置关系有两种;
③若线段AB与CD没有交点,则AB∥CD;④若a∥b,b∥c,则a与c不相交.
A.1个 B.2个 C.3个 D.4个
5.过一点画已知直线的平行线,则( )
A.有且只有一条 B.有两条; C.不存在 D.不存在或只有一条
二、填空题:(每小题3分,共15分)
1.在同一平面内,____________________________________叫做平行线.
2.若AB∥CD,AB∥EF,则_____∥______,理由是__________________.
3.在同一平面内,若两条直线相交,则公共点的个数是________;若两条直线平行,则公共点的个数是_________.
4.同一平面内的三条直线,其交点的个数可能为________.
5.直线L同侧有A,B,C三点,若过A,B的直线L1和过B,C的直线L2都与L平行,则A,B,C三点________,理论根据是___________________________.
三、训练平台:(每小题12分,共24分)
1. 已知直线a∥b,b∥c,c∥d,则a与d的关系是什么?为什么?
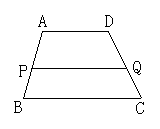
2.如图所示,梯形ABCD中,AD∥BC,P是AB的中点,过P点作AD的平行线交DC于Q点.
(1)PQ与BC平行吗?为什么?
(2)测量PQ与CQ的长,DQ与CQ是否相等?
四、提高训练:(每小题15分,共30分)
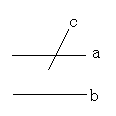
1. 如图所示,a∥b,a与c相交,那么b与c相交吗?为什么?
2.根据下列要求画图.
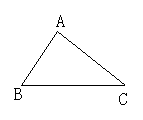
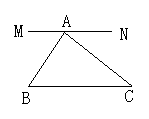
(1)如图(1)所示,过点A画MN∥BC;
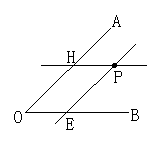
(2)如图(2)所示,过点P画PE∥OA,交OB于点E,过点P画PH∥OB,交OA于点H;
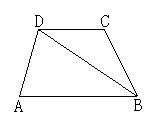
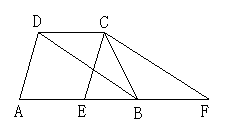
(3)如图(3)所示,过点C画CE∥DA,与AB交于点E,过点C画CF∥DB,与AB的延长线交于点F.

(1) (2) (3)
五、中考题与竞赛题:(共16分)
平面内有10条直线,无任何三条交于一点,欲使它们有31个交点,怎样才能办到?
答案:
一、1.A 2.D 3.C 4.B 5.D
二、
1.不相交的两条直线 2.CD EF 平行于同一条直线的两条直线平行 3.1个 0个 4.0个或1个或2个或3个 5.在一条直线上 过直线外一点有且只有一条直线与已知直 线平行
三、1.a与d平行,理由是平行具有传递性.
2. 解:(1)平行.
∵PQ∥AD,AD∥BC,
∴PQ∥BC.
(2)DQ=CQ.
四、1.解:b与c相交,
假设b与c不相交,
则b∥c,
∵a∥b
∴a∥c,与已知a与c相交矛盾.
3. 解:如图5所示.
(1) (2)
(3)
五、略.毛