平行线小结与复习 习题精选(一)
一、选择题
1.在同一平面内有![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 七条直线,如果
七条直线,如果![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ∥
∥![]() ,那么
,那么![]() 与
与![]() 的关系为( )
的关系为( )
A.平行 B.垂直
C.即不平行又不垂直 D.不能确定
2.已知命题:①对顶角的两条角平分线是一条直线;②两条直线相交构成的两组对顶角的角平分线互相垂直;③邻补角的两角平分线互相垂直;④如果两条直线平行,那么同位角的角平分线互相平行。上述四个命题中,真命题的个数是( )
A.1个 B.2个 C.3个 D.4个
3.如果一个角的两边与另一个角的两边分别平行,那么这两个角的关系是( )
A.相等 B.互余 C.互补 D.相等或互补
4.下列两个结论的真假情况为 ( )
(1)当两条直线被第三条直线截成的8个角中,有一对同旁内角互补时,所有的同位角都相等;
(2)两条直线被第三条直线所截,得到的同位角,内错角,同旁内角中有一对角都是直角,那么这两条直线一定平行。
A.真、真 B.真、假
C.假、真 D.无法确定
5.一张长方形的纸ABCD,如图,将C角折起到E处,作∠EFB的平分线FH,则∠HFG的大小是 ( )
A.锐角 B.直角
C.钝角 D.无法确定
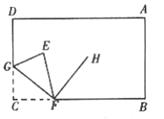
第5题图
6.在同一平面内,有三条直线a,b,c,如果a⊥c, b⊥c那么a与b的位置关系是( )
A.相交
B.平行
C.垂直
D.不能确定
7.下列命题中,是假命题的是
A.不相等的角不是对顶角
B.互补的两个角不一定相等
C.两点之间,线段最短
D.两条直线相交所构成的四个角中,任意的两个角都是对顶角
8.点C为线段AB上的一点,点D为BC的中点,若AD=5cm,则AC+AB为 ( )
A.8cm
B.10cm
C.12cm
D.无法计算
9.如图,OB⊥AE于O,OC、OD分别是∠AOB、∠BOE的平分线,图中互余的角共有( )对。
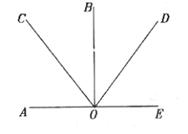
第9题图
A.3 B.4
C.5 D.6
10.若两个角的一边在同一条直线上,另一边互相平行,则这两个角的关系是 ( )
A.相等
B.互补
C.相等或互补
D.以上答案均不对
11.如图。同一平面内的三条直线两两相交,可得到线段、射线的条数分别是 ( )
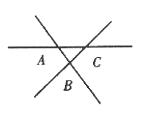
第11题图
A.0,6
B.3,6
C.3,12
D.0,3或6,12
二、填空题
12.从直线外一点向直线引垂线和斜线,则垂线段与斜线段的大小关系是__________。
13.三条直线AB,CD,EF交于点O,如图所示,∠AOC的对顶角是________,∠COB的对顶角是___________,∠EOB的对顶角是__________。
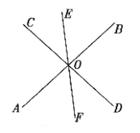
第13题图 第14题图
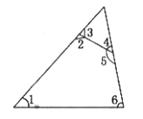
14.如图,∠1,∠2,∠3,∠4,∠5,∠6中是同位角的有_________,是内错角的有________,是同旁内角的有__________。
15.把命题“等角的补角相等”改写成“如果……那么……”的形式:________________。
16.利用一副三角板可以画出大于0°,但不大于180°的角共有_________个,其中可画出的锐角分别有_________。
三、解答题
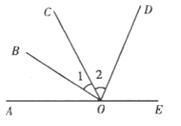
17.已知:如图,AE是一条直线,O是AE上一点,OB、OD分别是∠AOC、∠EOC的平分线。求证:OB⊥OD
第17题图
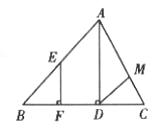
18.如图,AD⊥BC,EF⊥BC,∠AMD=104°, ∠BAC=76°
求证:∠BEF=∠ADM
第18题图 第19题图
19.(1)画图:(保留画图痕迹,不写作法)
①过C点作CD⊥AB,垂足为D;
②过D点作DE∥BC,交AC于E;
③取BC的中点G,作GF⊥AB,垂足为F。
(2)用量角器量一量∠CDE和∠BGF,它们相等吗?如果相等,请加以证明。(根据画图,写出已知,求证和证明)
20.如图,已知直线AB、CD被直线EF所截,∠1=∠2,∠3=∠4,∠1+∠3=90°.求证:AB∥CD。
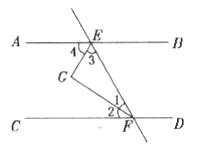
第20题图 第21题图
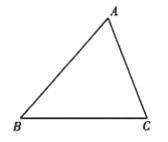
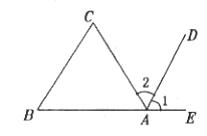
21.已知:如图,AD∥BC。求证:∠B+∠C+∠BAC=180°。
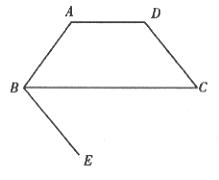
22.如图已知:AD∥BC,DC∥BE,∠A=∠D。
求证:∠CBE=∠ABC。
第22题图
答案
一、选择题
1.B 2.D 3.D 4.A 5.B 6.B 7.D 8.B 9.D 10.C
11.D
二、填空题
12.垂线段<斜线段;
13.∠BOD,∠AOD,∠AOF
14.同位角:∠1和∠3,∠4和∠6;内错角:∠2和∠4,∠3和∠5;同旁内角:∠1和∠2,∠5和∠6,∠1和∠6,∠2和∠5,∠3和∠4.
15.如果两个角相等,那么这两个角的补角也相等。
16.12;15°,30°,45°,60°,75°;
三、证明题
17.证明:∵OB、OD是∠AOC、∠EOC的平分线
∴∠1=![]() ∠AOC
∠AOC
∠2=![]() ∠COE
∠COE
∴∠1+∠2=![]() (∠AOC+∠COE)
(∠AOC+∠COE)
又∵AOE是一条直线,
∴∠AOE=180°
∴∠1+∠2=90°
∴OB⊥OD
18.证明:∵AD⊥BC,EF⊥BC(已知)
∴EF∥AD(垂直于同一条直线的两直线平行)
∵∠BEF=∠BAD(两条直线平行同位角相等)
∴∠AMD=104°
∠BAC=76°
∴∠BAC+∠AMD=180°(等式性质)
∴DM∥AB(同旁内角互补,两直线平行)
∴∠ADM=∠BAD(两线平行内错角相等)
∴∠BEF=∠ADM(等式性质)
19.(1)如图
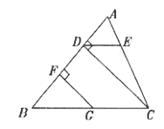
第19题图
(2)∠CDE=∠BGF
已知:如图CD⊥AB,垂足为D
DE∥BC交AC于E,G为BC的中点,
GF⊥AB,垂足为F
求证:∠CDE=∠BGF
证明:∵GF⊥AB,CD⊥AB(已知)
∴∠BFG=∠BDC=90°(垂直定义)
∴FG∥DC(同位角相等,两直线平行)
∴FGB=∠BCD(两直线平行,同位角相等)
∵DE∥BC(已知)
∴∠BCD=∠EDC(两直线平行,内错角相等)
∴∠CDE=∠BGF(等量代换)
20.证明∵∠AEF=∠3+∠4
∠CFE=∠1+∠2(如图)
又∵∠1=∠2,∠3=∠4(已知)
∴∠AEF=2∠3,∠CFE=2∠1(等量代换)
又∵∠1+∠3=90°(已知)
∴∠AEF+∠CFE=2(∠3+∠1)=180°(等式性质)
∴AB∥CD(同旁内角互补,两直线平行)
21.证明 ∵AD∥BC(已知)
∴∠1=∠B(两直线平行,同位角相等)
∴∠2=∠C(两直线平行,内错角相等)
∵∠1+∠2+∠BAC=平角=180°
∴∠B+∠C+∠BAC=180°(等量代换)
22.证明:∵AD∥BC
∴∠A+∠ABC=180°
同理,∠D+∠C=180°
又∵∠A=∠D
∴∠C=∠ABC
∵DC∥BE
∴∠C=∠CBE
∴∠CBE=∠ABC