初一数学期中试卷（三）
命题人：陆伟刚 审核：初一数学备课组 姓名： 得分：
一、精心选一选：(每题3分,共24分)
1．x=4是下列哪个方程的解（ ）
（A）3(x-2)=5(2x+3)（B）
（C）
（D）
2.若a＜0，关于x的不等式ax＋1的解集是( )
(A)x＞
(B)x＜
(C) x＞
(D) x＞
3．如果代数式
与x-1的和的值为0，那么x的值等于（ ）
（A）
（B）
（C）
（D）
4.在方程组
中，若未知数x、y满足x＋y＞0，则m的取值范围是（ ）
A、m＞3 B、m＜3 C、m≥3 D、m≤3
5.某推销员每周工资是200元,再加上该周销售额的5%作为奖金,在一周结束时,他挣了280元,那么该周销售员的销售额为( )
(A)800元 (B)1500元 (C)1600元 (D)2000元
6.下列各组数中,是方程组
的一个解的是( )
(A)
(B)
(C)
(D) 
7.已知
与
是同类项,那么( )
(A)
(B)
(C)
(D)
8.已知
是方程组
的解,则a、b的值分别是（ ）
（A）4，5 （B）4，3 （C）—4，3 （D）4，—3
二、耐心填一填：(每空2分,共24分)
9、小明假期外出旅行一周，这一周的日期之和是119，小明是 号回家的？
10、已知关于x的方程
的解为x=4,则m=
.
11、当a取 值时,代数式3－5a的值大于1。
12、不等式
的正整数解是
。
13、列不等式：
的一半与4的和两倍是非正数
。
14、已知
是方程5 x－( k－1)y－7 = 0的一个解，则k =_________。
15、不等式组
的最小整数解是
。
16、若
=0,则y=
。
17、方程2x + y = 5的正整数解为__________ 。
18、有一个三位数，它的十位数字比个位数字大2，百位数字比个位数字小2，三个数字的和的17倍等于原数，这个三位数是 。
19、在等式y=kx+b中,当x=4时,y=5； 当x= —2时,y=2，则k=
20、某市自来水收费实行阶梯水价,收费标准如下表所示,小王家3月份交水费48元,则小王家3月份用水 度.
| 月用水量 | 不超过18度部分 | 超过18度部分 |
| 收费标准(元/度) | 2.00 | 3.00 |
三、细心算一算：
21、解下列方程(组)：(每题4分，共计16分)
(1)
(2)
(3)
(4)
22、解下列不等式（组）：（每题3分，共计6分）
（1）
（2）
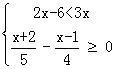
四、用心解一解：
23、已知不等式5（x-2）+8<6（x-1）+7的最小整数值为方程2x-ax=4的解，求a的值。（本题5分）
24、如果关于
的方程m+4x=3－2(x－2m)的解也是不等式组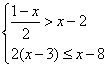
的一个解，求
的取值范围。（本题5分）
25、已知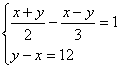
,求代数式
的值。（本题5分）
五、实践与探索：
26、由于用电量的剧增,某省最近新建甲、乙、丙三个电厂，这三个电厂的日供电量共计11.8万度,其中乙厂日供电量是甲厂日供电量的3倍,丙厂日供电量比甲厂日供电量的一半还多1万度.
(1)求这三个厂的日供电量各是多少万度?
(2)在修建甲厂厂房的工程中要运走600吨土石,市政公司派出A型、B型两种载重汽车，A型汽车6辆、B型汽车4辆，分别运5次，可把土石运完；或者A型汽车3辆、B型汽车6辆，分别运5次，也可把土石运完，那么每辆A型汽车、每辆B型汽车每次各运多少吨？（每辆汽车运土石都以标准载重量满载）（本题7分）
27、森林公园的门票每张10元，一次使用。考虑到人们的不同需求，也为了吸收更多的少游客，该公园除保留原有的售票方法外，还推出了一种“购买个人年票”的售票方法（个人年票从购买日起，可供持票者使用一年）。年票分A、B、C三类：A类年票每张120元，持票者是入该公园时，无需再购买门票；B类门票每张60元，持票者进入该公园时，需再购买门票，每次2元；C类门票每张40元，持票者进入该公园时，需再购买门票，每次3元。（1）如果您只选择一种购买门票的方式，并且您计划在一年中花80元在该公园的门票上，试通过计算，找出可使进入该公园的次数最多的购票方式。（2）求一年中进入该公园至少超过多少次时，购买A类年票比较合算。（本题8分）