七年级数学竞赛试题
（命题人：夏建平 考试时间：120分钟）
【第一部分（满分100分）】
一．选择题（每题5分，共35分）
1．图1中有8个完全相同的直角三角形，则图中长方形的个数是（ ）
A、5 B、6 C、7 D、8
2．若一条船顺流航速是逆流航速的3倍，这条船在静水中的航速与河水的流速之比是（ ）
A、3∶1 B、2∶1 C、1∶1 D、5∶2
3．某动物园有老虎和狮子，老虎的数量是狮子的2倍。每只老虎每天吃肉4.5千克，每只狮子每天吃肉3.5千克，那么该动物园的虎、狮平均每天吃肉（ ）
A、
千克 B、
千克 C、
千克 D、
千克
4．等腰三角形一腰上的高与另一腰的夹角为45°，则它的底角为（ ）
A、67°50′ B、135° C、67.5° D、以上均不对
5．在凸2004边形的所有内角中，锐角的个数最多是（ ）
A、0 B、1 C、3 D、5
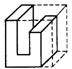
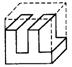
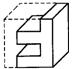
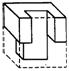
6．图2是正方体分割后的一部分，它的另一部分为下列图形中的( ).
 | |||||||||
 |  | ||||||||
 | |||||||||
 | |||||||||
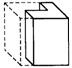图2 A B C D
7．画两条线段，它们除有一个公共点外不再有重叠的部分，在所得图中，设以所画线段的端点以及它们的公共点为端点的线段条数为n，那么对于各种可能的图形，不同的n值有（ ）
A、2个 B、3个 C、4个 D、多于4个
二．填空题（每空5分，共35分）
8．2003年10月15日9时9分50秒，我国“神舟”五号载人飞船准确进入预定轨道。16日5时59分，返回舱与推进舱分离，向地面返回。其间飞船绕地球飞行了60万千米。“神舟”五号载人飞船共巡天飞行了 秒，飞船的平均速度是 千米/秒。（答案取整数）
9．古希腊数学家把数1，3，6，10，15，21，……，叫做三角形数，它有一定的规律性，则第24个三角形数与第22个三角形数的差为 。
10．若对于有理数x、y规定x※y=ax+by，且2※3=11，5※（－3）=10，
则（－2）※
的值为
。
11．用三块正多边形的木板铺地，拼在一起并相交于一点的各边完全吻合，若其中两块木板的边数均为5，则第三块木板的边数为 。
12．甲对乙说：“当我的岁数是你现在的岁数时，你才4岁”；乙对甲说：“当我的岁数是你现在的岁数时，你将61岁”，则甲现在是 岁。
13．三位同学去买橡皮、铅笔和尺子，第一位同学买了3块橡皮、7支铅笔和1把尺子，共花了3.15元；第二位同学买了4块橡皮、10支铅笔和1把尺子，共花了4.20元；第三位同学买了1块橡皮、1支铅笔和1把尺子，花了_______元。
三．解答题（每题10分，共30分）
14．已知方程组
的解是
。求a∶b∶c的值。
15．如图3，
，
分别是∠EAB，∠DBC的平分线．若
，求∠BAC的度数。
16．阅读以下材料并填空：
平面上有n个点（n≥2），且任意三个点不在同一直线上，过这些点作直线，一共能作出多少条不同的直线？
⑴分析：当仅有两个点时，可连成1条直线；当有3个点时，可连成3条直线；当有4个点时，可连成6条直线；当有5个点时，可连成10条直线；……
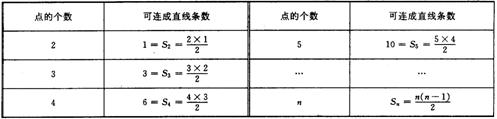⑵ 归纳：考察点的个数n和可连成直线的条数
，发现：
⑶
推理：平面上有n个点，两点确定一条直线．取第一个点A有n种取法，取第二个点B有（n－l）种取法，所以一共可连成n（n－1）条直线，但AB与BA是同一条直线，故应除以2，即
。
⑷
结论：．
试探究以下问题： 平面上有n（n≥3）个点，任意三个点不在同一直线上，过任意三点作三角形，一共能作出多少不同的三角形？
⑴ 分析：当仅有3个点时，可作 个三角形；当有4个点时，可作 个三角形；当有5个点时，可作 个三角形；……
⑵ 归纳：考察点的个数n和可作出的三角形的个数，发现：
⑶ 推理：
.
⑷ 结论： 。
【第二部分（满分30分）】
四．填空题（每题5分，共10分）
17．我们把形如
的四位数称为“对称数”，如1991、2002等．在2004～10000之间有_____个“对称数”．
18．已知三个质数x、y、z满足
，那么
的值等于______．
五．选择题（每题5分，共10分）
19．某月中有三个星期一的日期都是偶数，则该月的18日一定是（ ）
A、星期一 B、星期三 C、星期五 D、星期日.
20．已知a、b、c三个数中有两个奇数、一个偶数，n是整数。如果S=(a+n+2003)(b+2n+2004)(c+3n+2005), 那么( ).
A、S是偶数 B、S是奇数
C、S的奇偶性与n的奇偶性相同 D、S的奇偶性不能确定
六．解答题（本题10分）
21．如图4，△ABC的面积为1，BD∶DC=2∶1，E是AC的中点，AD与BE相交于点P，求四边形PDCE的面积。