七年级数学期末复习卷

七年级数学期末复习卷

一、选择题（每小题2分，共16分）

1．“神威1”计算机的计算速度为每秒次，这个速度用科学

记数法表示为每秒　　　　　　　　　　　　　　　　　　　　  （　　）（）384×10⁹ 次（）3.84×10⁹ 次（）384×10¹¹次（）3.84×10¹¹次

2．图中直线PQ、射线AB、线段MN能相交的是　　　　　　　 （　　）

（）　　　　　 　（）　　　　 　（）　　　　　　 （）

3．计算：，，，，，··· ···

归纳各计算结果中的个位数字规律，猜测的个位数字是　 （　　）

（） 1　　　　（） 3　　　　（） 7　　　　（） 5

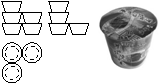4．若干桶方便面摆放在桌子上，实物图片左边所给的是它的三视图，则这一堆方便面共有（　　）

（）5桶　　　　　　 （）6桶

（）9桶　　　　　　 （）12桶

5．在数轴上与－3的距离等于5个单位的点表示的数是　　　　  （　　）

（）2　　　　（）－2　　　　（）－2和2　　（）－8和2

6．把两块三角板按右图所示那样拼在一起，则∠ABC的大小为　 （　　）

　　　　　　　　

（）90° （）100°　

（）120°（）135°

　　　　　　　　　　　　　　　 

7．如图，数轴上所标出的点中，相邻两点间的距离相等，则点A表示的数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 （　　）　　　　　 

（）30　　　（）50 　　　（）60　　　　（）80

 

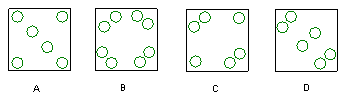
8．如图，将一块正方形纸片沿对角线折叠一次，然后在得到的三角形的三个角上各挖去一个圆洞，最后将正方形纸片展开，得到的图案是　 （　　）　　　　　　　　　　　　　　　　 　　　　　　　　　　　　　　　　　　　　　　　　　

二、填空题（每题2分，共14分）

9．－3的相反数是　　　　 ，倒数是　　　　 。

10．比较下列每组数的大小：　０　　　； －　　　　－３

11．计算：（1）12.42º=　　 º　　 ′　　　″；

(2) 2点30分时，时钟与分钟所成的角为　　　　度。

12．“x与的和的3倍”用代数式表示为_____________，当x＝3时，代数式的值为　　　　 。

13．写出一个满足下列条件的一元一次方程：①某个未知数的系数是－2；②方程的解是5；这样的方程是　　　　　　　　　　。

14．一根长长的电线上停了三只小鸟，我们可以近似地看作一条直线上有三个点、、（如图所示）

（1）请写出图中所有的线段，他们分别

是　　　　　　　　　　　 ；

（2）若点是线段的中点，，则　　　　　 。

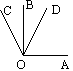15．如图，OA⊥OB, ∠BOC=30⁰, OD平分∠AOC，

则∠BOD= 　　　　。

三、计算与解方程（每题5分，共25分）

16．计算：

17．先化简，再求值：，其中x=

18. 解方程：4x-2=3-x

19．解方程：

20．一个角的余角比它的补角的还少40°，求这个角。

四、观察与比较（21题6分，22题4分，共10分）

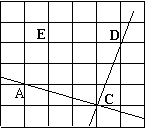
21．如图，在方格纸中，直线AC与CD相交于点C.

⑴ 过点E画直线EF，使EF⊥AC；

⑵ 分别表示图中三条直线之间的位置关系；

⑶ 根据你观察到的EF与CD间的位置关系，用一句话来解释你的结论

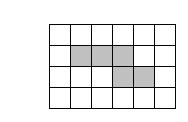
22．如图，某同学在制作正方体模型的时候，在方格纸上画出几个小正方形（图上阴影部分），但是一不小心，少画了一个，请你给他补上一个，可以组合成正方体，你有几种画法？请在图上用阴影注明，并标注不同画法的序号（如：①、②……）。

五、操作与解释（23题7分，24题5分，共12分）

23．老师要求同学们画一个75⁰的角，右图是小红画出的图形．

（1）　　　 检验小红画出的角是否等于75⁰；

（2）　　　 利用我们常用的画图工具，你有哪些检验方法？

（3）　　　 画此角的平分线oc

（4）　　　 解释图中几个角之间的相互关系．

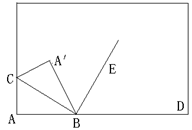
24．如图，将长方形纸片的一角折叠，使顶点A落在点A′处，BC为折痕，若BE是∠A′BD的角平分线，求∠CBE的度数，并说明理由。

六、探究与思考（25题7分，26题7分，共14分）

25．如图，点C在线段AB上，AC = 8 cm，CB = 6 cm，点M、N分别是AC、BC的中点。

（1）求线段MN的长；（2分）

（2）若C为线段AB上任一点，满足AC + CB = a cm，其它条件不变，你能猜想MN的长度吗？你能用一句简洁的话描述你发现的结论吗？（2分）

（3）若C在线段AB的延长线上，且满足ACBC = b cm，M、N分别为AC、BC的中点，你能猜想MN的长度吗？请画出图形，写出你的结论，并说明理由。（3分）

 

26．某班将买一些乒乓球和乒乓球拍，现了解情况如下：甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍。乒乓球拍每副定价30元，乒乓球每盒定价5元，经洽谈后，甲店每买一副球拍赠一盒乒乓球，乙店全部按定价的9折优惠。该班现需球拍5副，乒乓球若干盒（不小于5盒）。问：

（1）若购买的乒乓球为x盒，请分别写出在两家店购买这些乒乓球和乒乓球拍时应该支付的费用

（2）当购买乒乓球多少盒时，在甲、乙两店所需支付的费用一样？

（3）当购买15盒、30盒乒乓球时，请你去办这件事，你打算去哪家商店购买？为什么？

七、解决问题（本题9分）

 27．探索：在图1至图3中，已知△ABC的面积为a ．

（1）如图1，延长△ABC的边BC到点D，使CD=BC，连结DA．若△ACD的面积为S₁，则S₁=______（用含a的代数式表示）；

（2）如图2，延长△ABC的边BC到点D，延长边CA到点E，使CD=BC，AE=CA，连结DE．若△DEC的面积为S₂，则S₂=__________（用含a的代数式表示）；

（3）在图2的基础上延长AB到点F，使BF=AB，连结FD、FE，得到△DEF（如图12—3）．若阴影部分的面积为S₃，则S₃=__________（用含a的代数式表示）。

发现：

像上面那样，将△ABC各边均顺次延长一倍，连结所得端点，得到△DEF（如图3），此时，我们称△ABC向外扩展了一次．可以发现，扩展一次后得到的△DEF的面积是原来△ABC面积的　　　 倍。

应用：

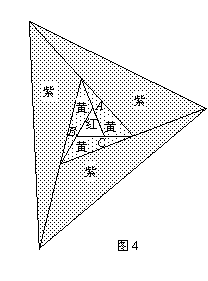要在一块足够大的空地上栽种花卉，工程人员进行了如下的图案设计：首先在△ABC的空地上种红花，然后将△ABC向外扩展三次（图4已给出了前两次扩展的图案）．在第一次扩展区域内种黄花，第二次扩展区域内种紫花，第三次扩展区域内种蓝花．如果种红花的区域（即△ABC）的面积是10平方米，请你运用上述结论求出：

（1）种紫花的区域的面积；

（2）种蓝花的区域的面积．

七年级数学期末复习卷答案

一、选择题

1．D　2.D　3.B  4.B　5.D　6.C  7.C　8.C　

二、填空题

9. 3；－1/3　10.＜；＞　11.12，25，12；105  12.3（x－4）；－3

13.答案不唯一　14.线段AB、AC、BC；100　15.30°

三、计算与解方程

16.10　 17.化简得4x² ，代入得1　 18.x＝1　19.x＝3/8　20.30°

四、观察与比较

21.（1）略（2）EF⊥AC，CD⊥AC，EF∥CD（3）垂直于同一条直线的两条直线互相平行

22.4种

五、操作与解释

23.（1）不等于（1分）（2）量角器量或三角板拼（2分）（3）略（1分）

（4）相等关系（2分），倍数关系（1分）

24. ∠CBE＝90°

六、探究与思考

25.（1）MN＝7cm（2分）（2）猜想MN＝1/2a（2分）（3）MN＝b/2（3分）

26.（1）甲店：30×5＋5×（x－5）＝5x＋125（元）（1分）

　　　 乙店：90%（30×5＋5x）＝4.5x＋135（元）（1分）

　 （2）5x＋125＝4.5x＋135，解得x＝20（3分）

　 （3）当购买15盒乒乓球时，应该在甲店购买；当购买30盒乒乓球时，应该在乙店购买（2分）

七、解决问题

27.解：探索：（3分）

（1）a ；（2）2a （3）6a ；

理由：∵CD=BC，AE=CA，BF=AB　

∴由（2）得　S_△ECD=2a，S_△FAE=2a，

S_△DBF=2a，

∴S₃=6a．　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

发现：　7（2分）　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

应用：（4分）

（1）（7²－7）×10=420（平方米）；　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

（2）（7³－7²）×10=2940（平方米）．