七年级上学期数学期末综合复习试卷（8）
一、填空题
1．今年哈尔滨市二月份某一天的最低气温为－19℃，最高气温为－3℃，那么这一天
的最高气温比最高气温高 ℃．
2．如果
与
互为相反数，那么
的值等于
．
3、大于 -
而小于1
的整数有是
4、3个连续奇数中，n为最大的奇数，则这3个数的和为 .
5、关于x的一元一次方程（
=m2的解为 .
6、（－
）
×（－
）
=
7、下列两个图是由几个相同的小长方体堆成的物体视图，那么堆成这个物体的小长方体最多有 个
 | |||
 | |||
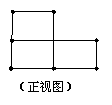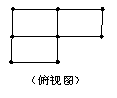8．小明同学在上楼梯时发现：若只有一个台阶时，有一种走法；若有二个台阶时，可以一阶一阶地上，或者一步上二个台阶，共有两种走法；如果他一步只能上一个或者两个台阶，根据上述规律，有三个台阶时，他有三种走法，那么有四个台阶时，共有 种走法．
9、一条
10、某军事行动中，对军队部署的方位，采用钟代码的方式来表示。例如，北偏东30°方向45千米的位置，与钟面相结合，以钟面圆心为基准，时针指向北偏东30°的时刻是1∶00，那么这个地点就用代码010045来表示。按这种表示方式，南偏东40°方向78千米的位置，可用代码表示为
二、选择题
11、下面计算正确的是 （ ）
（A）x
+ x =x
（B）5x— 2x = 3 （C）3x
+2y = 5xy （D）2xy—3yx= — xy
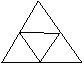12、如图，四个三角形均为等边三角形，将图形折叠得到的立体图形是 （ ）
（A）六面体 （B）三棱锥 （C）三棱柱 （D）四棱锥
13、把方程
中分母化整数，其结果应为（ ）
A、
Ｂ、０
Ｃ、
Ｄ、０
14、如果
的值为－1，则
的值为（ ）
A、1 B、
15．某种品牌的同一种洗衣粉有
三种袋装包装，每袋分别装有
元、2.8元、1.9元．三种包装的洗衣粉每袋包装费用(含包装袋成本)分别为0．8元、0．6元、0．5元．厂家销售三种包装的洗衣粉各1200千克，获得利润最大的是（ ）．
A．
种包装的洗衣粉 B．
种包装的洗衣粉C．
种包装的洗衣 D．三种包装的都相同
16．设“●、■、▲”分别表示三种不同的物体，如图所示，前两架天平保持平衡，如果要使第三架也平衡，那么“？”处应放“■”的个数为（ ）
 |  |
（1） （2） （3）
（A）5 （B）4 （C）3 （D）2
17．某年的某个月份中有5个星期三，它们的日期之和为80(把日期作为一个数，例如把22日看作22)，那么这个月的3号是星期（ ）
（A）日
（B）一
（C）二
（D）四
18．棱长是1cm的小立方体组成如图5所示的几何体，
那么这个几何体的表面积是（ ）
（A）36cm2 （B）33cm2
（C）30cm2 （D）27cm2
19．甲、乙两人以不变的速度在环形路上跑步，相向而行，每隔40秒相遇一次，已知甲跑一圈要60秒，则乙跑一圈所用的时间是（ ）秒
A、40 B、
20．某乡镇有甲、乙两家液化气站，他们的每罐液化气的价格、质和量都相同．为了促销，甲站的液化气每罐降价25%销售；每个用户购买乙站的液化气，第
罐按照原价销售，若用户继续购买，则从第
罐开始以7折优惠，促销活动都是一年．若小明家每年购买8罐液化气，则购买液化气最省钱的方法是（ ）
A．买甲站的 B．买乙站的C．买两站的都可以 D．先买甲站的1罐，以后再买乙站的
三、解答题21计算： [2－（－3）] ×[（－1）－（1－0.5×）]
22先化简，再求值3xy－[2xy－2（xy－1.5xy）+xy]+3xy其中x=3，y=－。
23解方程 
24如右图是由7块小正方体组成的立体图形，画出它的三视图
25、如图把一个边长为
（1）画出拼成梯形的两种拼法（2）画出拼成平行四边形的两种拼法。
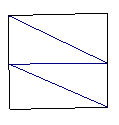①梯形示意图
②平行四边形示意图
26、．用水平线和竖直线将平面分成若干个边长为1的小正方形格子，小正方形的顶点，叫格点，以格点为顶点的多边形叫格点多边形。设格点多边形的面积为S，它各边上格点的个数和为
。
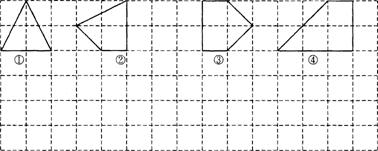
（1）上图中的格点多边形，其内部都只有一个格点，它们的面积与各边上格点的个数和的对应关系如下表，请写出S与之间的关系式。
答：S= 。
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和 | 4 | 5 | 6 | 8 | … |
（2）请你再画出一些格点多边形，使这些多边形内部都有而且只有2格点。此时所画的各个多边形的面积S与它各边上格点的个数和之间的关系式是：S=
。
（3）请你继续探索，当格点多边形内部有且只有
个格点时，猜想S与有怎样的关系？答：S=
。
四、应用题：
27.公司需在一个月（31天）内完成新建办公楼的装修工程。如果甲、乙两个工程队合作，12天完成，如果甲单独做8天，剩下的工作由乙独做18天可以完成。
（1）求甲、乙两个工程队单独完成工作的天数；
（2）如果请甲工程队施工，公司每日需付费用2000元，如果请乙工程队施工，公司每日需付费用1400元，在规定的时间内：A、请甲工程队单独完成此项工程；B、请乙工程队单独完成此项工程；C、请甲、乙两个工程队合作完成此项工程，试问：以哪一种方案花钱最少？
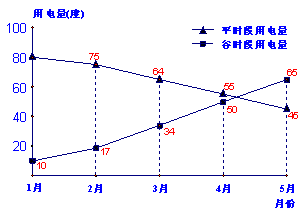
28、小明家使用的是分时电表，按平时段（6：00－22：00）和谷时段（22：00－次日6：00）分别计费，平时段每度电价为0.61元，谷时段每度电价为0.30元，小明将家里2005年1月至5月的平时段和谷时段的用电量分别用折线图表示（如图7），同时将前4个月的用电量和相应电费制成表格（如表1）
根据上述信息，解答下列问题：
（1） 计算5月份的用电量和相应电费，将所得结果填入表1中；
（2） 小明家这5个月的月平均用电量为 度；
（3） 小明家这5个月的月平均用电量呈 趋势（选择“上升”或“下降”）；这5个月每月电费呈 趋势（选择“上升”或“下降”）；
（4） 小明预计7月份家中用电量很大，估计7月份用电量可达500度，相应电费将达243元，请你根据小明的估计，计算出7月份小明家平时段用电量和谷时段用电量.
 |
月用电量（度） | 电费（元） | |
| 1月 | 90 | 51.80 |
| 2月 | 92 | 50.85 |
| 3月 | 98 | 49.24 |
| 4月 | 105 | 48.55 |
| 5月 |