七年级（下）数学暑期试卷（7）
(120分 120分钟)
| 题号 | 一 | 二 | 三 | 总分 | |||||||
| 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | ||||
| 得分 |
|
|
|
|
|
|
|
|
|
|
|
一、填空题：(每题2分,共20分)
1.∣－
∣ = ，
绝对值等于
的数是
。
2.
的平方根是______,
=________。
3.在△ABC中,已知两条边a=3,b=4,则第三边c的取值范围是_________。
4.点P（-2，1）向上平移2个单位后的点的坐标为 。
5．方程3x-5y=17,用含x的代数式表示y,y =_______,当x = -1时,y =______ 。
6.已知
是方程kx-2y-1=0的解,则k=________.
7 .不等式3x-12>0的解集是_______.
8. 若
，则x－y的值是_________。
9．某种商品的价格标签已经看不清，售货员只知道此种商品的进价为800元，商场为了促销打七折售出，但要保证利润率不低于5%，请你来帮助售货员重新填好价格标签至少应写 ___________元。
10.小王利用计算机设计了一个计算程序，输入和输出的数据如下表：
| 输入 | … | 1 | 2 | 3 | 4 | 5 | … |
| 输出 | … |
|
|
|
|
| … |
那么，当输入数据是8时，输出的数据是
二、选择题:(每题3分,共24分)
11. 如果a∥b, b∥c, d⊥a,那么（ ）
A.b⊥d B.a⊥c C.b∥d D.c∥d
12.点P(a,b)在第四象限,则点P到x轴的距离是( )
A.a B.b C.│a│ D.│b│
13.下列各式中是二元一次方程的是( )
A.3x-2y=9 B.2x+y=6z; C.
+2=3y
D.x-3=4y2
14.下列各组数中是方程组
的解为( )
A. 
B. 
C. 
D. 
15.已知a<b,则下列式子正确的是( )
A.a+5>b+5 B.3a>3b; C.-5a>-5b D.
>
16.如图,不能作为判断AB∥CD的条件是( )
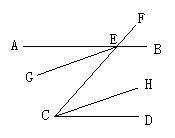A.∠FEB=∠ECD B.∠AEC=∠ECD; C.∠BEC+∠ECD=180° D.∠AEG=∠DCH
17．有下列说法：
（1）无理数就是开方开不尽的数；
（2）无理数是无限不循环小数；
（3）无理数包括正无理数、零、负无理数；
（4）无理数都可以用数轴上的点来表示。
其中正确的说法的个数是（ ）
A．1 B．2 C．3 D．4
18.下列各式中,正确的是( )
A.±
=±
B.±=; C.±=±
D.=±
三、解答题:(76分)
19.解下列方程组:(12分)
(1) 
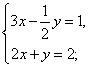
(2) 
20. 求不等式组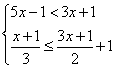
的整数解。(6分)
21. 甲、乙两人共同解方程组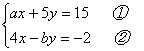
,由于甲看错了方程①中的
,得到方程组的解为
；乙看错了方程②中的
,得到方程组的解为
。试计算
的值.(8分)
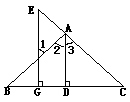
22．(6分)填空：如图，AD⊥BC于D，EG⊥BC于G，∠E =∠1，可得AD平分∠BAC。
理由如下：
∵AD⊥BC于D，EG⊥BC于G（ 已知 ）
∴∠ADC =∠EGC = 90°（ ）
∴AD∥EG（ ）
∴∠1 = （ ）
= ∠3 （ ）
又∵∠E = ∠1（ ）
∴∠2 =∠3（ ）
∴AD平分∠BAC（角平分线的定义 ）。
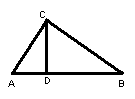
23.(12分) 如图，在直角三角形ABC中，∠ACB=90°，CD是AB边上的高，AB=13cm，BC=12cm，AC=5cm， 求:
(1)作出△ABC的边AC上的中线BE
(2)△ABC的面积和CD的长；
(3)作出△BCD的边BC边上的高DF，当BD=11cm 时，试求出DF的长。
 |
24. A、B两地相距20千米，甲从A地向B地前进，同时乙从B地向A地前进，两小时后二人在途中相遇，相遇后，甲返回A地，乙仍向A地前进，甲回到A地时，乙离A地还有2千米，，求甲、乙二人的速度。(10分)
25．(10分)某电视台黄金时段的2分钟广告时间内，计划插播长度为15秒和30秒的两种广告。15秒广告每播一次收费0.6万元，30秒的广告收费1万元，若要求每种广告播放不少于2次。
（1） 两广告的播放的次数有几种安排方式？
（2） 电视台选择哪种方式播放收益较大？
26．(12分)修筑高速公路经过某村，需搬迁一批农户，为了节约土地资源和保持环境，政府统一规划搬迁建房区域，规划要求区域内绿色环境占地面积不得高于区域总面积的20%，若搬迁农民建房每户占地150m2，则绿色环境面积还占总面积的40%；政府又鼓励其他有积蓄的农户到规划区域建房，这样又有20户加入建房，若仍以每户占地150m2计算，则这时绿色环境面积只占总面积的15%，为了符合规划要求，又需要退出部分农户。问：（1）最初需搬迁的农户有多少户？政府规划的建房区域总面积是多少？
（2）为了保证绿色环境占地面积不少于区域总面积的20%，至少需要退出农户几户？
参考答案:
一、1. ，± 2.1 提示:│x-1│+│x-2│=(x-1)+(2-x)=1.
3.1<c<7 提示:两边之差小于第三边,两边之和大于第三边.
4.（－2 ，3） 5.
,－ 4 6. 3 7.x>4 8. 4 9. 1200 10.
二、11.A 12.D 13.A 14.A 15.C 16.D 17.B 18. A
|
|
y = ①
(2) 2x +
5y = 25 ①
2x + y = 2 ② 4x + 3y = 15 ②
解：①×2得 ： 解：①×2得：
6x － y = 2 ③ 4x ＋10y =50 ③
②＋③得： ③－②得：
8x = 4 7y = 35
X = y
= 5
把 X = 代入②得：
把 y = 5代入①得：
y = 1 x = 0
|
|
∴ x = 0
y = 1 y = 5
20.
|
㎝ ,(3)
㎝24.解：设甲、乙二人的速度分别是x千米/时，y千米/时，依题意得：
2(x＋y) = 20
2(x－y) = 2
|
y =4.5
25.解：（1）设15秒广告播放x次，30秒广告播放y次，依题意得：
15x + 30y = 120
则 x = 8 – 2y
∵ x,y为不小于2的正整数
|
|
y = 3 y = 2
所以有两种播放方式：①15秒的广告播放2次，30秒的广告播放3次，②15秒的广告播放4次，30秒的广告播放2次
(2) 方式①的收费
0.6×2＋1×3 = 4.2（万元）
方式②的收费：
0.6×4＋1×2 = 4.4（万元）
所以选择方式收益较大
26．解：(1)设最初需搬迁的农户有x户，政府规划建房区域总面积是y㎡，仍题意得：
|
y – 150(x + 20) = 15％y
|
解得 x = 48
y = 12000
(2)设至少需退出z户，则
12000 – 150(48 + 20 – z )≥ 12000×20％
解得
Z ≥ 4