7.2二元一次方程组的解法
一、选择题
1.在代数式![]() 中,当
中,当![]() 时,它的值是
时,它的值是![]() ;当
;当![]() 时,它的值是3,则
时,它的值是3,则![]() 的值是
( )
的值是
( )
(A)![]() ;
(B)
;
(B)![]() ;
;
(C)![]() ;
(D)
;
(D)![]()
2.代数式![]() 当
当![]() ;它的值 是7;当
;它的值 是7;当![]() 时,它的值是4,
时,它的值是4,
那么 ( )
![]()
![]()
![]() (A)
(A) ![]() (B)
(B) ![]()
![]() (C)
(C) ![]() (D)
(D) ![]()
![]() 3.若方程组
3.若方程组 ![]() 无解,则
无解,则![]() 的值是
( )
的值是
( )
(A)![]() ;
(B)
;
(B) ![]() ;
(C)
;
(C) ![]() ;
(D)
;
(D)![]() .
.
4.已知![]() 和
和![]() 是同类项,则
是同类项,则![]() 与
与![]() 的值为
( )
的值为
( )
![]()
![]()
![]() (A)
(A) ![]() ;
(B)
;
(B) ![]() ;
;
![]() (C)
(C) ![]() ;
(D)
;
(D) ![]() .
.
5.关于x,y的方程组![]() 的解是二元一次方程3x+2y=14的一个解,那么m的值是( )
的解是二元一次方程3x+2y=14的一个解,那么m的值是( )
(A)1; (B) -1; (C)2; (D)-2
6.已知方程![]() ,则x,y的值是(
)
,则x,y的值是(
)
![]()
![]()
![]()
![]()
二、填空题
7.已知方程![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]() ,用含
,用含![]() 的代数式表示
的代数式表示![]() ,则
,则![]()
8.若![]() 与
与![]() 是同类项,则
是同类项,则![]() 的值是______________.
的值是______________.
![]() 9.如果方程组
9.如果方程组 ![]() 的解是正数,则整数
的解是正数,则整数![]() 的值是____________________.
的值是____________________.
![]()
![]() 10.已知方程
10.已知方程![]() 的两个解是
的两个解是 ![]() ,
,
![]() 则
则![]()
三、解答题
11.解下列方程组:
![]() (1)
(1) ![]()
![]() (2)
(2) 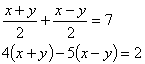
![]() (3)
(3) ![]()
![]() (4)
(4) ![]()
![]() (5)
(5) ![]()
(6)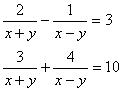
![]() 12.已知方程组
12.已知方程组 ![]() 的解能使等式
的解能使等式![]() 成立,求
成立,求![]() 的值.
的值.
![]()
![]() 13.已知关于的方程组
13.已知关于的方程组 ![]() 和
和 ![]() 的解相同,求
的解相同,求![]() 的值.
的值.
答案
一、1. C 2. B 3. B 4. A
5.C 6.A
二、7. ![]() 8.
8. ![]()
9. ![]() 10.
10. ![]()
![]() 三、11.(1)解:原方程组可化为
三、11.(1)解:原方程组可化为 ![]() ①
①
![]()
![]() ②
把①代入②得
②
把①代入②得![]()
![]() ,把
,把![]() 代入①得
代入①得![]() ,故方程组的解为
,故方程组的解为 ![]()
![]() (2)解:原方程组可化为
(2)解:原方程组可化为 ![]() ①
①
![]()
![]() ② 解得
② 解得 ![]()
(3)①-
②,得![]() ,所以
,所以![]() 把
把![]() 代入①,得
代入①,得![]() ,
,
![]() 所以
所以![]() ,所以
,所以 ![]()
![]() .
.
(4)①×3-
②×2得![]() 把
把![]() 代入①得
代入①得
![]()
![]()
![]()
![]()
![]()
![]() (5)原方程可化为
(5)原方程可化为 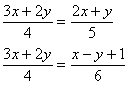 即
即 ![]() ①
①
![]()
![]() ②,②-①得
②,②-①得![]() ,把
,把![]() 代入①得
代入①得![]()
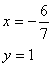
![]() (6)令
(6)令![]() 则
则 ![]() ①
①
![]()
![]()
![]() ②.
①×4+②得
②.
①×4+②得 ![]() 把
把![]() 代入①得
代入①得![]() ,故得
,故得 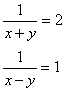 即
即 ![]() ③
③
![]()
![]() ④,③+④得
④,③+④得![]() 把
把![]() 代入④得
代入④得![]() .经检验:
.经检验: 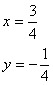 是原方程的解
是原方程的解
![]() 12.
12. ![]() ①
①
![]()
![]() ② ①- ②×2
得
② ①- ②×2
得![]() ,所以
,所以![]() 把
把![]() 代入②得
代入②得![]() ②所以
②所以![]() ,所以
,所以 ![]() ,把
,把![]() 代入得
代入得![]() ,解之得
,解之得![]() ,解之得
,解之得![]() .
.
![]()
![]() 13.因为两个方程组的解相同,所以解方程组
13.因为两个方程组的解相同,所以解方程组 ![]() 得
得 ![]() ,
,
![]() 将
将 ![]()
![]() 分别代入
分别代入![]() 和
和![]() 得
得 ![]() ①
①
![]()
![]() ② 由②- ①×2得
② 由②- ①×2得![]() 将
将![]() 代入①,得
代入①,得![]() ,所以
,所以 ![]()
![]()