《三角形的初步知识》单元检测
班级 学号 姓名
一、填空题（每小题4分，共24分）
1．在ΔABC中，∠A=45°，∠B=30°，则∠C=__________。
2．在直角三角形中，已知一个锐角为25°，则另一个锐角的度数为__________。
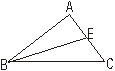
3、如图，在ΔABC中，BE是边AC上的中线，已知AB=4cm，AC=3cm，
BE=5cm，则ΔABC的周长是_______cm。
 |  | ||||||
 | |||||||
 | |||||||
第3题 第4题 第5题 第6题
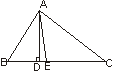
4．如图，在ΔABC中，AD是ΔABC的高，AE是ΔABC的角平分线，已知
∠BAC=82°，∠C=40°，则∠DAE=________。
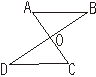
5．如图，AC与BD相交于点O，已知OA=OC，OB=OD，则ΔAOB≌ΔCOD的理由是_________。
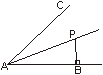
6．如图，点P是∠BAC的平分线上一点，PB⊥AB于B，且PB=5cm，则P到AC边的距离是________cm。
二、选择题（每小题4分，共20分）
1．下列各组线段中，能组成三角形的是……………………………………（ ）
A、a=6.3cm，b=6.3cm，c=12.6cm B、a=1cm，b=2cm，c=3.5cm
C、a=2.5cm，b=3cm，c=5cm D、a=5cm，b=7cm，c=12cm
2．在ΔABC中，已知∠A=∠B，∠C=40°，则∠A的度数为………………（ ）
A、40° B、70° C、100° D、140°
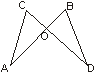3、如图，已知ΔOCA≌ΔOBD，并且∠A=30°，∠AOC=80°，
则∠B的度数为…………………………………………（ ）
A、30° B、80°
C、90° D、70°
4．直线L⊥线段AB于点O，且OA=OB，点C为直线L上一点，且有CA=8cm，则CB的长度为………………………………………………………………( )
A、4cm B、8cm C、16cm D、无法求出
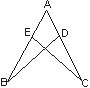5．如图，点D、E分别在AC、AB上，已知AB=AC，添加下列条件，
不能说明ΔABD≌ΔACE的是…………………………（ ）
A、∠B=∠C B、AD=AE
C、∠BDC=∠CEB D、BD=CE
三、补充填空题：（共10分）
1．
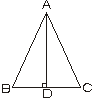如图，在ΔABC中，AD⊥BC于D，BD=CD，则∠B=∠C。
请完成下面的说理过程。
解：∵AD⊥BC（已知）
∴∠ADB=______________=Rt∠（垂线的意义）
当把图形沿AD对折时，射线DB与DC___________
∵BD=CD (_________________________________)
∴点B与点_______重合
∴ΔABD与ΔACD_________
∴∠B=∠C （___________________________________________）
2．
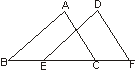如图，点B、E、C、F在同一直线上，且AB=DE，AC=DF，BE=CF，请将下面说明ΔABC≌ΔDEF的过程和理由补充完整。
解：∵BE=CF （_____________）
∴BE+EC=CF+EC
即BC=EF
在ΔABC和ΔDEF中
AB=________ （________________）
__________=DF（_______________）
BC=__________
∴ΔABC≌ΔDEF （_____________）
四、画图题（共10分）
1．已知∠α和∠β，（如图），求作∠BAC，使∠BAC=∠α+∠β。
注：保留作图痕迹，不要求写画法，但要写出结论。
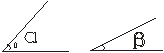
2．已知∠α，∠β和线段a，用直尺和圆规作ΔABC，使∠A=∠α，∠B=∠β，AB=a。
五、解答题（36分）
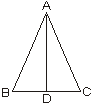
1．（6分）如图，在ΔABC中，AC=AB，AD是BC边上的中线，则AD⊥BC，请说明理由。
 |
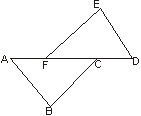
2．（6分）如图，已知AB=DE，BC=EF，AF=DC，则∠EFD=∠BCA，请说明理由。
 |
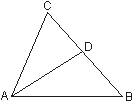
3．（8分）如图，AE是ΔABC的角平分线，已知∠B=45°，∠C=60°，求下列角的大小： （1）∠BAE （2）∠AEB
 |
4．（8分）如图，在ΔABC中，D是边BC上一点，AD平分∠BAC，在AB上截取AE=AC，连结DE，已知DE=2cm，BD=3cm，求线段BC的长。
 |
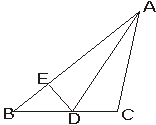5．（8分）如图，ΔABC的两条高AD、BE相交于H，且AD=BD，试说明下列结论成立的理由。
（1）∠DBH=∠DAC；
（2）ΔBDH≌ΔADC。
 |
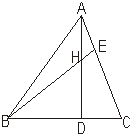