初一数学5月份月考试卷
一、选择题：（每小题3分，共30分）
1.已知
，
都是方程
的解，则k和b的值是（ ）
A. 
B.
C. 
D. 
2.下列各式是二元一次方程的个数是（ ）
（1）
（2）
（3）
（4）
（5）
（6）
A.1个 B.2个 C.3个 D.4个
3．不等式4（x
2）＞2（3x + 5）的非负整数解的个数为( )
A．0个 B．1个 C．2个 D．3个
4.若x+y=6，x－y=2，则xy=（ ）
A.12 B.16 C.4 D.8
5. 以
为解的方程组是（ ）
A. 
B. 
C. 
D. 
6. 如果方程组
的解与方程组
的解相同，则a、b的值为（ ）
A.
B. 
C. 
D. 
7．若不等式组的解集为1≤x≤3，则图中表示正确的是（ ）
A． 
B．
C． 
D．
8．若方程
的解是负数，则
的取值范围是（ ）
A．
B．
C．
D．
9．不等式
的解集为
，则 的值为（ ）
A．4
B．2
C．
D．
10．不等式组
的解集是（ ）
A．
≥
1 B．＜5
C．1≤＜5 D．≤1或＜5
二、填空题：（每小题3分，共30分）
11.已知
，用含
的代数式表示
，用含
的代数式表示
.
12．已知x的与5的差不小于3，用不等式表示这一关系式为
。
13.已知二元一次方程
，写出满足方程的两个解
.
14.若
是二元一次方程，则
, 
.
15．某饮料瓶上有这样的字样：Eatable Date 18 months. 如果用x （单位：月）表示Eatable Date（保质期），那么该饮料的保质期可以用不等式表示为 。
16.在3x+4y=9中，如果 2y=6, 那么 x=
17．若方程mx+ny=6的两个解是x=1,y=1;x=2,y= -1,则m= , n= 。
18.如果︳x-2y+1︱+ ︳x+y-5︱= 0,那么 x= , y= 。
19．当x
时，式子3x5的值大于5x + 3的值。
20．阳阳从家到学校的路程为2400米，他早晨8点离开家，要在8点30分到8点40分之间到学校，如果用x表示他的速度（单位：米/分），则x的取值范围为 。
三、解答题：（40分）
21. ① 用适当的方法解下列方程组. （每小题3分，共6分）
⑴
⑵
②、解不等式
，并把它的解集表示在数轴上。（3分）
③．解不等式组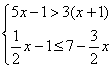
（3分）
22.已知方程组
的解x与y的和为7，求k的值（4分）
四、实际应用（每小题10分，共20分）
23．用16元买了60分、80分两种邮票共22枚。60分与80分两种邮票各买了多少枚？（5分）
24．小颖家每月水费都不少于15元，自来水公司的收费标准如下：若每户每月用水不超过5立方米，则每立方米收费1. 8元；若每户每月用水超过5立方米，则超出部分每立方米收费2元，小颖家每月用水量至少是多少？（5分）
25．学校将若干间宿舍分配给七年级一班的女生住宿，已知该班女生少于35人，若每个房间住5人，则剩下5人没处住；若每个房间住7人，则还有一间房住的人数少于4人。有多少间宿舍，多少名女生？（6分）
26.某商场计划用90000元从厂家购进50台电视机，已知该厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，,台2100元，丙种每台2500元.其中甲种电视机每台可获利150元，乙种电视机每台可获利200元，丙种电视机每台可获利300元.若该商场同时购进其中两种不同型号的电视机共50台，用去90000元. （8分）
⑴请你帮助设计进货方案；
⑵从销售利润来看，选择哪种方案？通过计算最后确定方案.
（二）参考答案
1．B 2．B 3．A 4．D 5．B 6．C 7. D 8. C 9.
B 10. C
11. y=
,x=
12. 
≥3 13. 不唯一 14. -
15. x≤18 16. -1 17.
4 , 2 18. 3 , 2 19. x＜4
20.60≤x≤80 21. ① ⑴ x=
, y=-
⑵x=
, y=-
② x≥4，数轴表示略。③ 2＜x≤4
22. k=16 23. 60分邮票8枚 , 80邮票14枚 24．8立方米 25. 5间房，30名女生。
26. (1) 方案1: 甲种25台, 乙种25台; 方案2: 甲种35台, 乙种15台; (2) 选择第二种方案。