相交线、平行线自我测试题
(时间:60分 满分:100分)
一. 选择题:(每小题3分,共24分)
在下列各题的四个备选答案中,只有一个是正确的.
1.在同一平面内,两条直线可能的位置关系是 [
]
A. 平行 B. 相交 C. 相交或平行 D. 垂直
2.下列说法正确的是 [ ]
A. 若两个角是对顶角,则这两个角相等.
B. 若两个角相等,则这两个角是对顶角.
C. 若两个角不是对顶角,则这两个角不相等.
D. 以上判断都不对.
3.下列语句正确的是 [ ]
A. 两条直线被第三条直线所截,同旁内角互补.
B. 互为邻补角的两个角的平分线互相垂直.
C. 相等的角是平行线的内错角.
D. 从直线外一点作这条直线的垂直线段叫点到直线的距离.
4.点到直线的距离是 [ ]
A. 点到直线上一点的连线 B. 点到直线的垂线
C. 点到直线的垂线段 D. 点到直线的垂线段的长度
5.判定两角相等,不对的是 [ ]
A. 对顶角相等
B. 两直线平行,同位角相等
C. ∵∠1=∠2,∠2=∠3,∴∠1=∠3
D. 两条直线被第三条直线所截,内错角相等
6.两个角的两边分别平行,其中一个角是60°,则另一个角是 [ ]
A. 60° B. 120°
C. 60°或120° D. 无法确定
7.如图,AB⊥CD,垂足为B,EF是经过B点的一条直线,已
知∠EBD=145°,则∠CBE,∠ABF的度数分别为 [ ]
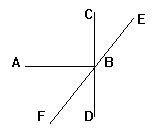
A. 55°,35° B. 35°,55°
C. 45°,45° D. 25°,55°
8.已知:如图,下面判定正确的是 [ ]
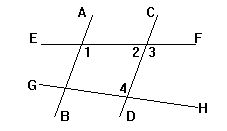
A. ∵∠1=∠2,∴AB∥CD
B. ∵∠1+∠2=180°,∴AB∥CD
C. ∵∠3=∠4,∴AB∥CD
D. ∵∠1+∠4=180°,∴AB∥CD
二. 填空题:(每小题4分,共24分)
1. 如果a∥b,b∥c,则______∥______,因为________.
2.下列语句①直角都相等,②延长AB到C,使BC=2AB,
③若∠α>∠β,则∠α+∠γ>∠β+∠γ,④期中考试谁夺魁,
⑤等角的余角相等.是真命题的有________(只填序号).
3.将“平行于同一直线的两条直线平行”改写成“如果……那么……”
的形式.
4.自钝角的顶点引角的一边的垂线,把这个钝角分成两个角的度数之比
是3∶1,则这个钝角的度数是___________.
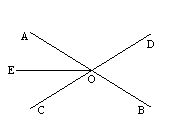
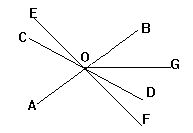
5.如图BE,CF相交于O,OA,OD是射线,其中构成对顶角的角是
_____________________________.
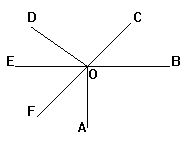
6.如图,直线AB,CD相交于O,OE平分∠AOC,∠EOC=35°,
则∠BOD=___________.
三. 填注理由:(本题10分)
如图,已知:直线AB,CD被直线EF,GH所截,且∠1=∠2,
求证:∠3+∠4=180°.
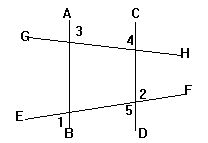
证明:∵∠1=∠2 ( )
又∵∠2=∠5 ( )
∴∠1=∠5 ( )
∴AB∥CD ( )
∴∠3+∠4=180° ( )
四. 计算题:(每小题6分,共18分)
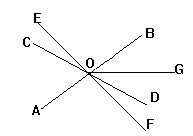
1.已知:如图,AB,CD,EF三直线相交于一点O,且OE⊥AB,
∠COE=20°,OG平分∠BOD,求∠BOG的度数.
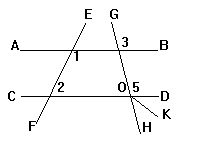
2.已知:如图,∠1+∠2=180°,∠3=100°,OK平分∠DOH,
求∠KOH的度数.
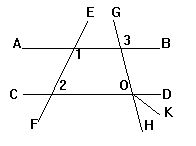
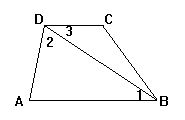
3.已知:如图,∠1=40°,∠2=65°,AB∥DC,
求:∠ADC和∠A的度数.
五. 证明题:(每小题8分,共24分)
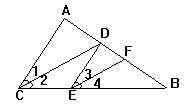
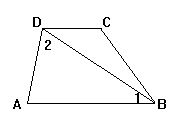
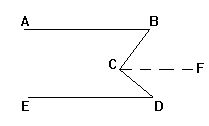
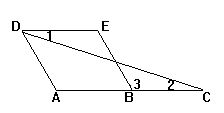
1.如图:已知∠BCD=∠B+∠D,求证:AB∥ED.
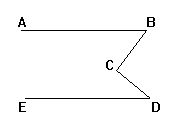
2.已知:如图AD∥BE,∠1=∠2,求证:∠A=∠E.
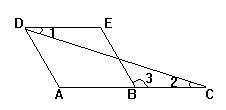
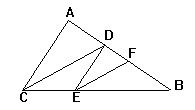
3.已知:如图,CD平分∠ACB,AC∥DE,CD∥EF,
求证:EF平分∠DEB.
相交线和平行线自我测试题参考答案
(时间:60分,满分:100分)
一. 选择题:(每小题3分,共24分)
1. C 2. A 3. B 4. D
5. D 6. C 7. B 8. B
二. 填空题:(每小题4分,共24分)
1. a,c,如果两条直线都和第三条直线平行,那么这两条直线也互
相平行;
2. ①,③,⑤;
3. 如果两条直线都和第三条直线平行,那么这两条直线也互相平行;
4. 120°;
5. ∠BOC和∠EOF,∠BOF和∠COE;
6. 70°.
三. 填注理由:(本题10分)
已知;
对顶角相等;
等量代换;
同位角相等两直线平行;
两直线平行同旁内角互补.
四. 计算题:(每小题6分,共18分)
1. 解:∵OE⊥AB,∠COE=20°(已知)
∴∠BOD=180°-90°-20°=70°
OG是角平分线
∴∠BOG=35°
2. 解:∠1+∠2=180°(已知)
AB∥CD(同旁内角互补,两直线平行)
∠3=∠5(两直线平行,同位角相等)
∠DOH=180°-∠5
∠3=100°(已知)
∴∠DOH=80°
OK平分∠DOH
∴∠KOH=40°
3. 解:∵AB∥DC(已知)
∴∠1=∠3(两直线平行,内错角相等)
∠1=40°,∠2=65°(已知)
∠ADC=∠2+∠3=40°+65°=105°
∠A+∠ADC=180°(两直线平行,同旁内角互补)
∠A=180°-∠ADC=75°
五. 证明题:(每小题8分,共24分)
1. 证明:过C作CF∥AB
∴∠B=∠BCF(两直线平行,内错角相等)
∵∠BCD=∠B+∠D(已知)
∴∠D=∠FCD(等量减等量差相等)
∴CF∥ED(内错角相等,两直线平行)
∴AB∥ED(两条直线都和第三条直线平行,那么这两条直
线也互相平行)
2. 证明:∵∠1=∠2(已知)
∴DE∥BC(内错角相等,两直线平行)
∴∠E=∠3(两直线平行,内错角相等)
∵AD∥BE(已知)
∴∠A=∠3(两直线平行,同位角相等)
∴∠E=∠A(等量代换)
3. 证明:∵AC∥DE(已知)
∴∠ACB=∠DEB(两直线平行,同位角相等)
∵CD∥EF(已知)
∴∠2=∠4(两直线平行,同位角相等)
∴∠1=∠3(等量减等量,差相等)
∵∠1=∠2(已知)
∴∠3=∠4(等量代换)
∴EF平分∠DEB