初一数学单元检测试卷
（范围：第六章—第八章的第2节，满分：100分 2007、3）
一、填空题（每空2分，共26分）
1、点P（-2，5）在第 象限
2、点A（-3m，m+8）在x轴上，则m=
3、在x+3y=2中用含x的代数式表示y，则y=
4、已知点P（a,-3）,Q(2,b)且PQ∥y轴，则a=
5、当x=1，y=2 是二元一次方程mx-3y=1的解时，m=
6、等腰三角形的两边长分别为3和8，则它的周长是
7、已知一个多边形的内角和是2340º，则这个多边形的边数为
8、下列正多边：（1）正三角形 （2）正方形 （3）正边多形 （4）正六边形，其中用一种多边形能镶嵌成平面图案的是
9、若∣x+y-1∣+(2x+y+1)2=0，对x= ，y=
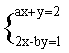10、已知（m+1）x∣m∣+y是关于x、y为未知数的二元一次方程，则m =
11、甲、乙二人解方程组 甲看错 a得解 ，乙看错b得解
若都不看错解为
12、某单位办公室的地板由三种正多边形的小木块铺成，设这三种正多边形的边数分别为x、y、z(注，每个顶点周围有且仅有三块不同的木块)，则 + + =
二、选择题（每小题3分，共30分）
13、二元一次3x+5y=1的解是（ ）
A、任何一个有理数对 B、无穷多个数对，但不是任意一个有理数对
C、仅有一个有理数对 D、有限个数有理数对
14、已知x轴上的点P到y轴的距离为3，则P点的坐标为（ ）
A、（3，0 ） B、（0，3） C、（3，0）或（-3，0） D、（0，3）或（0，-3）
15、三角形的两边分别为3和5，则周长L的范围是（ ）
A、6＜L＜15 B、6＜L＜16
C、11＜L＜13 D、10＜L＜16
16、三角形的三个外角的比为2：3：4，则这个三角形一定是（ ）
A、锐角三角形 B、直角三角形 C、钝角三角形 D、无法确定
17、把点P1（2，-3）向右平移3个单位长度再向下平移2个单位长度到达点P2处，则P2的坐标是（ ）
A、（5，-1） B、（-1，-5） C、（5，-5） D、（-1，-1）
18、点P（-a2-1， a2+1 ）关于x轴对称的点P′在第（ ）象限
A、一 B、二 C、三
D、四
19、如图AC⊥BC，CD⊥AB DE⊥BC，下列 说法中不正确的是（ ）
A、AC是△ABC的高 B、DE是△BCD的高
C、DE是△ABE的高 D、AD是△ACD的高
20、甲、乙两人相距42千米，如果相向而行，2小时相遇，如果同向而行乙14小时才能追上甲，则甲、乙两人的速度分别是每小时（ ）
A、12千米 9千米 B、11千米 10千米
C、10千米 11千米 D、9千米 12千米
21、一个多边形除了一个内角之外其余各角的和为2750 º，则这一内角是（ ）
A、130 º B、140 º C、155 º D、120 º
22、若方程组 4x+3y=1 的解x与y互为相反数，则a的值为（ ）
ax-（a-1）y=3
A、1 B、2 C、3 D、4
三、解答题（第1题8分，第2—第7题每小题6分，共44分）
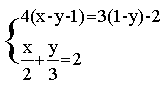
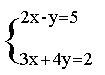1、解下列方程组
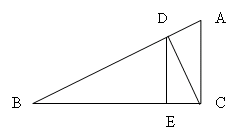
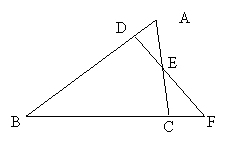2、如图已知点F是△ABC的BC边延长线上的一点，DF⊥AB于D，DF与AC交于点E，∠A=60 º，∠F=35 º，求∠ACB和∠DEC的度数。
3、在某校举行的足球比赛中规定：胜一场得3分平一场得1分，负一场得0分，某班足球队参加了12场比赛共得22分，已知这个队只输了2场，那么此队胜几场，平几场？
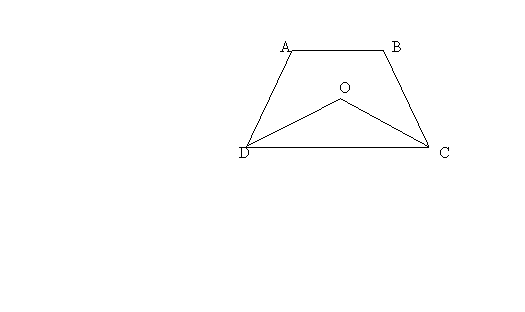
4、如图，四边形ABCD中，∠A+∠B=230 º，且∠ADC、∠DCB的平分线相交于点O，求∠COD的度数。
 | |||
 | |||
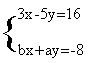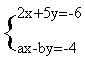5、已知方程组 和方程组 的解相同
求：（2a+b）2007的值。
6、已知点A（0，-5），B（0，3）
（1）在x轴上找一点C，使之满足S△ABC=8 求点C的坐标。
（2）在坐标平面上找一点C，能满足S△ABC=8的点C有多少个？这些点有什么规律？
7、如图在下列三个图形中，已知∠ABC=12 º，Q=90 º
（1）在图（1）中，若α1=β1，则∠A=
（2）在图（2）中，若α1=β1，α2=β2，则∠A=
（3）在图（3）中，α1=β1，α2=β2，α3=β3，αn=βn，(n是大于等于的自然数)则∠A=