初一数学第二学期期中考试试题

初一数学第二学期期中考试试题

　　　　　　　 

　  说明：1.可以使用计数器，但未注明精确度的计算问题不得采用近似计算，建议根据题型特点把握好使用计算器的时机。

　　 　2．本试卷满分100分，在90分钟内完成。相信你一定会有出色的表现。加油哦！

一.填空题（每题2分，共20分）

1. 多项式5a²b－ab＋3a－1中，是 　　　　 (几次几项式)，

2.　计算　　　；

3.  _{=　　　 .}

4.　4.52⁵精确到　　　　　 位。

5.自从扫描隧道显微镜发明以后，世界上便诞生了一门新兴的学科，这就是“纳米技术”.已知1纳米=米，则2.25纳米用科学记数法表示为　　　　 米 .（结果保留两位有效数字）

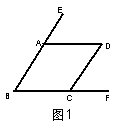
6．已知：如图1，要得到AB//CD，则需要的条件　　　　　　

(填一个你认为正确的条件即可）

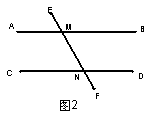7．已知：如图2，直线、与直线相交于、，

且//。若，则度

8．已知 , 那么 a =　　　　。

9．小明同学将(图3)中的阴影部分（边长为m的大正方形

中有一个边长为n的小正方形），拼成了一个长方形（如图4），

比较两图阴影部分的面积，可以得到的结论是　　　　　　　 （用含m,n的式子表示）

10．小强将10盒蔬菜的标签全部撕掉了。现在每个盒子看上去都一样。但是她知道有三盒玉米，两盒菠菜，四盒豆角，一盒土豆。她随机地拿出一盒并打开它。盒子里面是玉米的概率是　　　 。

二.选择题:(每小题3分,共21分.每小题只有一个正确的选项符合题意)

1. 下列句子中的数，是近似数的是　　　　　　　　　　　　　　　  【　　 】

A.　　 某市有中学106所。　

B.　　 我国有34个省级行政单位。　　　　　　　 

C.　　 七年级三班男生23人，女生21人。 　　　　　　　　

D.　　 一双没洗的手，带有各种细菌80000万个。

2. 某天数学课上老师讲了整式的加减运算，小颖回到家后拿出自己的课堂笔记，认真地

复习老师在课堂上所讲的内容，她突然发现一道题目：

（2a²+3ab-b²）-（-3a²+ab+5b²）=　5a² 　　　 - 6b²，

空格的地方被墨水弄脏了，请问空格中的一项是　　　　　　　　　　　 【　　 】

A、+2ab　　　 B、+3ab　　 C、+4ab　　　　D、-ab

3. 长荆铁路使武汉至宜昌的铁路全程只有260千米，它的百万分之一，相当于【　　 】A、你自己的身高　　　　　　　　　 　　　 B、一张课桌的长度　　

C、数学期中考试卷的宽度　　　　D、黑板长度

4. 下列说法:①两条直线被第三条直线所截，内错角相等；②相等的角是对顶角；③互余的两个角一定都是锐角；④互补的两个角一定有一个为钝角，另一个角为锐角。其中正确的有　　　　　　　　　　　　　　　　　　　　　　　　　　　 【　　 】

A. 1个　　　　 B.　2个　　　 C.　3个　　　　　　 D.4个　　　　　　　　　　　　

5．如图5在下列条件中, AD//BC的条件是: 【　　 】　

A、　　　　　　　　　 B、

C、　　　 D、

6．下列运算中,正确的个数有　　　　　  【　　 】　　　　  图5

①；②；③；

④；⑤; ⑥

 A. 1个　　　　 B.　2个　　　 C.　3个　　　　　　 D.4个

Ë	²	ù
²	ù	²
ù	²	Ë

ù

7.如图6，小颖有一个卡片藏在9块瓷砖中的某一块下面（每块瓷砖除图案外其它均相同），那么卡片藏在　　　 瓷砖下的概率为  【　　 】

A. 　　　　　　B.　　　　　  C. 　　　　　D.

图6

三. 解答题(要写出解答步骤.共59分)

 1.计算(每题5分，共20分.)

 (1)　　　　(2).

解：　　　　　　　　　　　　　　　　　　 解：

(3).　 　　　 (4). 　

解：　　　　　　　　　　　　　　　　　　 解：

2.(6分)化简求值： 其中

　解：

3. 阅读填空：（11分）

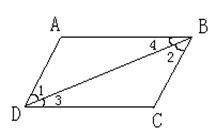(1)如图7，请你完成小颖和小明的说理过程：

小颖：

因为AD与BC是平行的，所以

∠１＝_______，理由是__________________.

小明：　　　　　　　　　　　　　 　　　　　　　　

∠3＝∠4 → ______∥_______ → ∠Ａ＋______＝180º　　图7

　 其中第一步的理由是________________________________

第二步的理由是_____________________________________

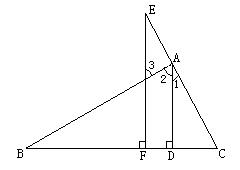 (2)如图：已知：AD⊥BC于D，EF⊥BC于F，∠1=∠3，　　

求证 ：AD平分∠BAC。

证明：∵AD⊥BC 于D　　　　　　　　　　　　　　　　　　　 　　　　　　　 

　　　EF⊥BC于F（已知）　　　　　　　　　　　　　　　　　　　　　　　 

 ∴∠EFB=∠ADB=90º（　　　　　　　　　　 ）

 ∴AD∥EF（　　　　　　　　　　　　　　　　 ）　　　　　　　　　　  图8

 ∴∠2＝∠______（　　　　　　　　　　　　　　　　　　  ）　　　　　　　  

 又∵∠3＝∠1（已知）　　　　　　　　　　　　　　　　　　　　　　　　　　　

　 ∴∠1＝∠2

∴AD平分∠BAC（　　　　　　　　　　　　  ）

4．作图题（尺规作图，不写作法，保留作图痕迹。）（6分）

（下面有2小题，请你任选一题做,）

（1）如图，已知∠α，求作 ∠β，使它等于∠α补角的2倍。

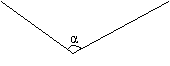 (2）如图，小颖走在一条比直的小路上，小明站在小路外的一点C处，你能帮助小明设计一条路线，使这条路线与小颖所走的路线平行吗？

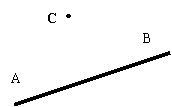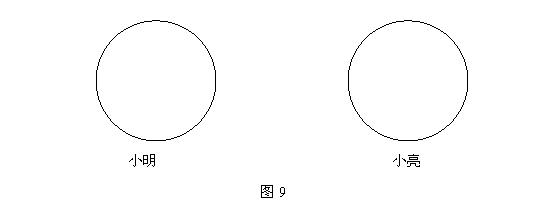
5.(6分)小明和小亮在操场上做一个游戏，每人拿一个转盘（如图9），转动手中的转盘，指针落在区域内的数字是几就往前跨几步，交替转动，看谁先到达操场的另一端。这个游戏对两人公平吗？为什么？如果游戏不公平，你能重新设计，使游戏公平吗？你把设计结果画在图10中并说明游戏规则。

　　　　　　　　 　　　　　　　　　　　

　　　　　　 

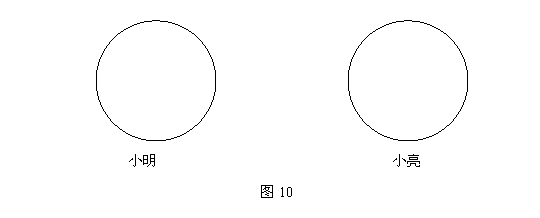
6．下表列出了中国、美国、日本、印度、澳大利亚5个国家1996年的人口总数和淡水资源总量的情况：（10分）

	中国	美国	日本	印度	澳大利亚
人口总数（万）	122389	26519	12576	94561	1831
淡水资源总量 （万立方千米）	279.3	245.5	54.6	204.9	33.9

(1)　  分别估计这五个国家1996年的人均淡水资源量是多少立方千米（保留3个有效数字），并求出它们的比（精确到个位）。

(人均淡水资源量=淡水资源总量÷人口总数)

解:　

(2) 用你学过的统计图的制作方法，作一个统计图来形象地表示五个国家的人均淡水资源量。观察此图,你发现了哪些信息?

解：

(3)　深圳市人均淡水资源占有量仅为全国的四分之一,是全国7个严重缺水的城市之一,对此你有何感想?

解：