初一数学仿真训练（第6周）
班别： 姓名： 学号：
一填空题1、方程
的“解”的步骤如下，错在哪一步（ ）
A． 2(x－1)－(x+2)=3(4－x) B．2x－2－x+2=12－3x
C． 4 x=12 D．x=3
2.下列方程括号内的数是这个方程的解的是( )
A.
B.
C.
D.
3.方程
的解是
,则
等于( )
A.
B.
C.
D.
4．一个长方形的长是宽的4倍多2厘米，设长为x厘米，那么宽为( )厘米。A、
B、4x-2 C、
D、
5.某班分两组去两处植树,第一组22人,第二组26人.现第一组在植树中遇到困难,需第二组支援.问第二组调多少人去第一组才能使第一组的人数是第二组的2倍?设抽调
人,则可列方程( )
A.
B.
C.
D.
6、方程x+2y=6的自然数解有 组 A ) 2 B) 3 C)4 D )5
7.若
是一元一次方程，则
A ) 1 B) 2 C) -1 D) -2 .
8.当x= 时，代数式
的值比–4小1
A ) 1 B) 2 C) -1 D) -2 .
9. 方程组
的解是
A) 
B) 
C) 
D) 
10.把面值1元的纸币换成面值为1角或2角的硬币，则换法共有
A ) 3种 B) 4种 C) 5种 D) 6种
二、选择题： 11.如果方程ay-2x=3的解是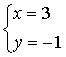
，那么a= .
12．若方程
，则用含
的代数式表示为
。
13.若代数式
与
是同类项,则m= ， n= .
14 由方程组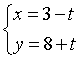
可得x、y满足的关系式为
。
15、有20道竞赛题，对于每一题，答对得6分，答错或不答扣3分，小明在这次竞赛中的得分为八十多分，则小明答对了 题
三、解答题
解方程（组）16、 
17、
18.
19、
20、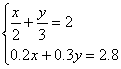
四、解答题：21、某种商品的进价为400元，出售时标价为600元，商店准备打折销售，但要保持利润为5%，那么应打多少折？
22、我国民间流传着许多趣味算题，此类算题或者是把枯燥的数学问题改编成有趣的小故事，或者是用朗朗上口的诗歌形式表达出来。下面介绍一题，请你解出本文的问题。 甲乙隔溪牧羊，二人相互商量。
甲得乙羊九只，多乙一倍正当。
乙说得甲九只，两人羊数一样。
甲乙羊各几只？让你算个半晌。
23、一件工程，甲单独做需20小时完成，乙单独做需12小时完成。现由甲单独做4个小时，剩下的部分由甲、乙合作，还需几小时完成？完成任务时，甲做了总工程的几分之几？
24、某商店采购一批灯管，每根13元，在运输过程中不慎损坏了12根，出售时的单价为15元，售完后共获利1020元，则一共购进灯管多少根？
25、一架飞机所带的燃料最多可以用6小时，飞机去时顺风，每小时可以飞1500千米，飞回时逆风，每小时可以飞1200千米，问：这架飞机最多能飞多少千米就需要往回飞？
26、某厂第二车间的人数比第一车间的人数的80%少30人，如果从第一车间调10人到第二车间，那么第二车间的人数就是第一车间的75%，问这两个车间各有多少人？
27、客车和货车分别在两条平行的铁轨上行驶，客车长150米，货车长250米.如果两车相向而行，那么从两车车头相遇到车尾离开共需10秒钟；如果客车从后面追货车，那么从客车车头追上货车车尾到客车车尾离开货车车头共需要1分40秒.求两车的速度.
28、某商场计划拨款9万元从厂家购进50台电视机．已知该厂家生产三种不同型号的电视机，出厂价分别为：甲种每台1500元，乙种每台2100元，丙种每台2500元．（1）若商场同时购进其中两种不同型号电视机共50台，用去9万元，请你研究一下商场的进货方案；
(1) 若商场销售一台甲种电视机可获利150元，销售一台乙种电视机可获利200元，销售一台丙种电视机可获利250元．在同时购进两种不同型号电视机的方案中，为使销售时获利最多，你选择哪种进货方案?
(2) 若商场准备用9万元同时购进三种不同型号的电视机50台，请你设计进货方案．