初一数学期末复习讲义2 编写人:古 光
复习内容:第6章平面图形的认识(一)—线段、射线、直线、平行线、垂直
一、知识点复习及例题选讲
1、知识点1 :(1)线段、射线、直线的异同点:
| 名 称 | 图形及表示法 | 不同点 | 联系 | 共同点 | ||
| 延伸性 | 端点数 | 与实物联系 | ||||
| 线段 | 真尺 | 线段向一方延长就成射线,向两方延长就成直线 | 都是直的线 | |||
| 射线 | 电筒发生的光线 | |||||
| 直线 | 笔直的公路 | |||||
(2)线段的统计方法:看线上端点的个数为n个,则有n(n-1)/2条线段。
射线的统计方法:直线上端点的个数为n个,则有2n条射线;其中有2条不好用图中字母表示。射线上端点的个数为n个,则有n条射线;其中有1条不好用图中字母表示。
![]() 例 1、已知点A、点B、点C是直线上的三个点,则下图中有_____条线段,它们是
,有____射线,能用图中字母表示的有
,有_________条直线,它们是
,。
A
B C
例 1、已知点A、点B、点C是直线上的三个点,则下图中有_____条线段,它们是
,有____射线,能用图中字母表示的有
,有_________条直线,它们是
,。
A
B C
例 2、判断题:射线AB与射线BA表示同一条直线. ( )
例 3、根据图形,下列说法:①直线AC和直线BD是不同的直线;②直线AD=AB+BC+CD;③射线DC和射线DB不是同一条射线;④射线AB和射线BD不是同一条射线;⑤线段AB和线段BA是同一条线段。其中正确的是 ( )
A、1个 B、2个 C、3个 D、4个
2、知识点2 :(1)两点之间的所有连线中,线段最短。(2)两点之间线段的长度叫做这两点之间的距离。(3)直线外一点与直线上各点连接的所有线段中,垂线段最短。直线外一点到这条直线的垂线段的长度叫做这点到这条直线的距离。
例 1、下列四个生活、生产现象:①用两个钉子就可以把木条固定在墙上;②植树时,只要定出两棵树的位置,就能确定同一行树所在的直线;③从A地到B地架设电线,总是尽可能沿着线段AB架设④把弯曲的道路改直,就能缩短路程。其中可用“两点之间,线段最短”的道理来解释的现象有__________.
例 2、判断题:连结两点的线段叫做两点之间的距离.( )
 例 3、
如图,从A地到B地有①、②、③三条路可以走,每条路长分别为
例 3、
如图,从A地到B地有①、②、③三条路可以走,每条路长分别为![]() (图中
(图中![]() 、
、![]() 表示直角),则第_________条路最短,另两条路的长短关系为__________________。
表示直角),则第_________条路最短,另两条路的长短关系为__________________。
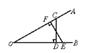 例4、如图3,CD⊥OB于D,EF⊥OA于F,则C到OB的距离是______,E到OA的距离是______,O到CD的距离是______,O到EF的距离是______.
例4、如图3,CD⊥OB于D,EF⊥OA于F,则C到OB的距离是______,E到OA的距离是______,O到CD的距离是______,O到EF的距离是______.
例5、直线![]() 外一点
外一点![]() 与直线
与直线![]() 上三点的连线段长分别为
上三点的连线段长分别为![]() ,
,
则点![]() 到直线
到直线![]() 的距离是(
)
的距离是(
)
![]() 、
、![]()
![]() 、
、![]()
![]() 、不超过
、不超过![]()
![]() 、大于
、大于![]()
3、知识点3 :(1)过一个点可以画无数条直线 (2)经过两点有一条直线,并且只有一条直线 (3)过同一平面上的三个点可以画一或三条直线(不在一直线上可画3条直线,在一直线上可画1条直线)
例 1、如果你想将一根细木条固定在墙上,至少需要钉2个钉子,这一事实说明了____________________________________。
例 2、平面上有三个点,可以确定直线的条数是( )
A、1 B.2 C.3 D.1或 3
4、知识点4 :平分一条线段的点叫线段的中点
例 1、延长线段MN到P,使NP=MN,则N是线段MP的______点,MN=_____MP,MP=___NP
![]() 例 2、如图,C、D是线段AB上的两个点,CD=8cm,M是AC的中点,N是DB的中点,MN=12cm,那么线段AB的长等于_______cm
例 2、如图,C、D是线段AB上的两个点,CD=8cm,M是AC的中点,N是DB的中点,MN=12cm,那么线段AB的长等于_______cm
A M C D N B
5、知识点5 :(1)在同一平面内,不相交的两条直线叫做平行线,在同一平面内,两条直线的位置关系是:_______________(2)如果两条直线相交成直角,那么这两条直线互相垂直。其中一条直线叫做另一条直线的垂线。(3)如果两条直线都与第三条直线平行,那么两条直线互相平行。例 1、判断题:同一平面内相交的两条直线必定相互垂直 ( )
例 2、如图,在方格纸中,直线AC与CD相交于点C(本题10分)
(1) 过点E画直线EF,使EF⊥AC;
(2) 分别表示(1)中三条直线之间的位置关系;
(3) 根据你观察到的EF与CD间的位置关系,用一句话来解释你的结论.
![]()
|
![]()
|
|
|
![]()
![]() 例 1、判断题:(1)经过一点,有且只有一条直线与已知直线平行, ( )(2)经过直线外一点,有且只有一条直线与已知直线垂直。 ( )
例 1、判断题:(1)经过一点,有且只有一条直线与已知直线平行, ( )(2)经过直线外一点,有且只有一条直线与已知直线垂直。 ( )
二、练习
1、过两点可确定一条直线,过A、B、C、三点的直线的条数是
A、 1条 B、3条 C、1条或2条 D、1条或3条
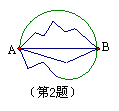
2.如图,从A到B有多条道路,人们往往走中间的直路,而不会走其他的曲折的路,这是因为
![]() A.两点之间线段最短
B.两条直线相交只有一个交点
A.两点之间线段最短
B.两条直线相交只有一个交点
C.两点确定一条直线 D.其他的路行不通
3.手电筒发出的光线,给我们的形象似
A、直线 B、射线 C、线段 D、折线
4、如图:直线MN上有两点A、B,则图中有射线_____条,线段有________条。
5、不在同一直线上的四点最多能确定 条直线。
6、固定一根木条在墙上至少需要_____个钉子。
![]() 7、如图,在平面内有A、B、C三点
A
7、如图,在平面内有A、B、C三点
A
![]() (1)画直线AC、线段BC、射线BA;
C
(1)画直线AC、线段BC、射线BA;
C
(2)取线段BC的中点D,连接AD;
![]() (3)延长线段CB到E,使EB=CB,并连接AE。
B
(3)延长线段CB到E,使EB=CB,并连接AE。
B
(4)过点A画AF//BC,过点B画BG垂直AC,垂足为G。
8、已知线段AB=2cm,延长AB到C,使BC=2AB,若D为AB的中点,求DC的长。
![]() 9、如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点,求线段MN的长。
9、如图,线段AB=8cm,C是线段AB上一点,AC=3.2cm,M是AB的中点,N是AC的中点,求线段MN的长。
A N C M B
10、点M在线段AB上,给出下列四个条件,其中不能判定点M是线段AB中点的是 ( )
A、AM=BM B、AB=2AM C、BM= AB D、AM+BM=AB
![]() 11、如图,C、D是线段AB上的两个点,CD=8cm,M是AC的中点,N是DB的中点,MN=12cm,那么线段AB的长等于_______cm
11、如图,C、D是线段AB上的两个点,CD=8cm,M是AC的中点,N是DB的中点,MN=12cm,那么线段AB的长等于_______cm
A M C D N B
 初一数学期末复习讲义
编写人:古 光
初一数学期末复习讲义
编写人:古 光
 复习内容:第6章平面图形的认识(一)—角、余角、补角、对顶角
复习内容:第6章平面图形的认识(一)—角、余角、补角、对顶角
一、知识点复习及例题选讲
1、知识点1 :角的表示方法有几种注意点是什么?
例 1、如图共有几个角?分别表示出来?
例 2、如图共有几个小于平角的角?分别表示出来?
2、知识点2:角的度量单位是:__________________;
10=__________‘ 1’=_____________"
例 1、![]() =
= ![]()
![]()
例 2、![]()
![]()
例 3、用一付三角板,可以拼出多少种不同的角?
3、知识点3:角平分线的定义
例 1、已知![]() AOB = 80o,OC是
AOB = 80o,OC是![]() AOB的平分线,则
AOB的平分线,则![]() AOC= 。
AOC= 。
例 2、把一个平角分成三等份,两旁两个角的角平分线所成的角的度数为 ( )
A、150° B、120° C、90° D、60°
4、知识点4:(1)如果两个角的和是_________,这两个角叫做互为余角,简称互余,其中的一个角是另一个角的余角。(2)如果两个角的和__________,这两个角叫做互为补角,简称互补,其中一个角叫做另一个角的补角。(3)同角(或等角)的余角_________ 同角(或等角)的补角___________。(4)一个锐角的补角比这个角的余角大 。
例 1、若∠1和∠2互为余角,∠1和∠3互为补角,∠2和∠3的和等于周角的三分之一,那么∠1、∠2、∠3的度数分别为()
A.75○、15○、105○ B、60○、30○、120○C.50○、40○、130○ D、70○、20○、110○
例 2、若∠α+∠β=90°, ∠β+∠γ=90°,则∠α与∠γ的关系是( )
A、互余 B、互补 C、相等 D、没有关系
例 3、(1)75°40′30″的余角是_______(用度分秒表示);补角是_______(用度表示);
(2)、若∠1+∠2=90°,∠1+∠3=90°,则∠2=∠3的理由是____________________。
若∠1+∠2=180°,∠3+∠4=180°,且∠1=∠3,则∠2=∠4的理由是________________
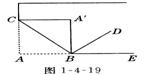
例 4、如图l-4-19所示,将书页折过去,使角顶点 A落在A′处,BC为折痕,BD
为∠A′BE的平分线,求∠CBD的度数.
5、知识点5:(1)______________________ ,我们把这样的两个角叫做互为对顶角。其中一个角叫做另一个角的对顶角。(2)、对顶角的性质:_________________.
 例
1、两条直线相交于一点,有 对对顶角,三条直线相交于一点,有 对对顶角,
例
1、两条直线相交于一点,有 对对顶角,三条直线相交于一点,有 对对顶角,
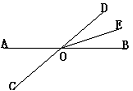
例 2、如图,直线AB、CD相交于点O,OE平分∠BOD,
∠AOD-∠DOB=72°,求∠AOC和∠DOE的度数。
例 3、下列图中,∠1与∠2是对顶角的图是 ()
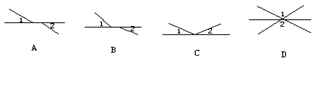 |
6、知识点6:方位角
例 1、在海上,灯塔位于一艘船的北偏东40度方向,那么这艘船位于这个灯塔的( )
A 南偏西50度方向 B南偏西40度方向
C 北偏东50度方向 D北偏东40度方向
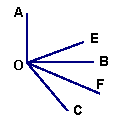
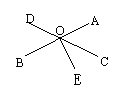
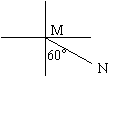 例 2、如右图所示,由M观测N的方向是
例 2、如右图所示,由M观测N的方向是
A、北偏西60° B、南偏东60°
 C、北偏西30° D、南偏东30°
C、北偏西30° D、南偏东30°
二、练习
1、判断题(1)、两条射线组成的图形叫做角.( )
(2).角的大小与角的两边的长短无关.( )
(3)如果两个角的和是一个直角,这两个互为补角;( )
(4)若有两个角相等,则这两个角是对顶角;( )
(5)如果有两个角互余,那么这两个角的和一定是90°。( )
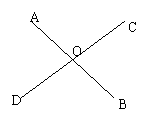
2、如右图所示,直线AB、CD 相交于O点,∠AOC和
 ∠BOD的和是220°,则∠BOC=____.
∠BOD的和是220°,则∠BOC=____.
3、如图,![]() ,
,![]() ,点B、O、D在同一直线上,
,点B、O、D在同一直线上,
则![]() 的度数为( )
的度数为( )
A. ![]() B.
B.![]() C.
C.![]() D.
D.![]()
 4、计算:①1.5°= ′=
″;②450″= ′= °;
4、计算:①1.5°= ′=
″;②450″= ′= °;
 ③90°- 54°48′6″=
.
③90°- 54°48′6″=
.
5、如右图,OA⊥OB,直线CD过点O,
且∠AOC=50°, 则∠DOB= °
6、右上图中,以O为顶点的角有 个,
它们分别是 .
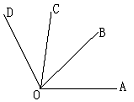 7、已知∠AOB=50°,以OB为一边画∠BOC=20°,
7、已知∠AOB=50°,以OB为一边画∠BOC=20°,
则∠AOC=______°.
8、时钟时间是2:30时,时针与分针的夹角是____°
9、如图,已知OC平分∠BOD,
∠AOD=110°,∠COD=35°,
则∠AOB=_____°,∠AOC=____°
10如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°
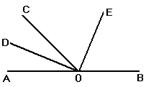 (1)请你数一数,图中有多少个小于平角的角;
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)试判断OE是否平分∠BOC,并说明理由.
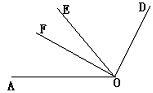 |
11、如图,OE是∠AOD的平分线,OF⊥OD,垂足为O,
∠EOF=19°,求∠AOD的度数。
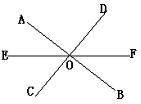
12、如图,直线AB、CD、EF,相交于点O,∠AOF=3∠FOB,
∠AOC=90°,求∠EOC的度数。
13、一个角的补角比它的余角的3倍少12度,求这个角的度数。
14、如图,直线![]() 相交于点
相交于点![]() ,
,![]() ,
,
求∠DOA的度数。