初一数学期末复习讲义 编写人：古 光
复习内容：第5章走进图形世界—立体图形、图形的变化
一、知识点复习及例题选讲
1、知识点1 ：常见立体图形的认识与分类
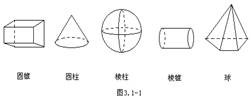
例 1、如图3.1-1，将下列图形与对应的图形名称用线连接起来：
例 2、埃及金字塔类似于几何体 （ ）
A、圆锥 B、圆柱 C、棱锥 D、棱柱
2、知识点2 ：点动成线，线动成面，面动成体
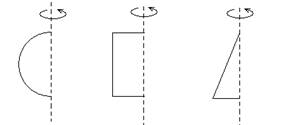
例 1、下列图形绕虚线旋转一周，形成一个几何体，在对应横线上，写出几何体的名称。
例 2、点动成线，线动成面，面动成体，请举实例说明。
3、知识点3 ：棱锥、棱柱的棱、侧棱、顶点、底面的概念与统计
1）、n棱锥有 条棱， 个顶点， 个面。n棱柱有 条棱， 个顶点， 个面。
例 1、4棱锥有 条棱， 个顶点， 个面。5棱柱有 条棱， 个顶点， 个面。
例 2、一个棱锥有7个面，这是 棱锥，有 个侧面。
例 3、棱柱的 长相等，上下底面是 的多边形，侧面是 。
例 4、下图3.1-8是图（1）的正方体切去一块，得到图（2）~（5）的几何体，
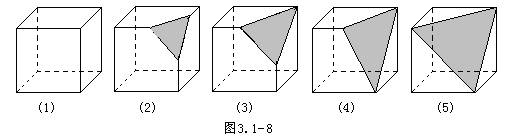
它们各有多少个面？多少条棱？多少个顶点？
4、知识点4：欧拉公式的内容
例 1、将正方体的面数记为f，边数记为e，顶点数记为v，则f+v-e= （ ）
A、1 B、2 C、3 D、4
例 2、有一个几何体，有9个面，16条棱，那么它有 个顶点。
5、知识点5：图形的变化方式：平移、旋转、翻折
例 1、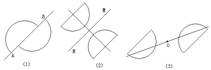
下列图形都是由半圆经过变化而得到的，请说出它们最简单的变化过程。
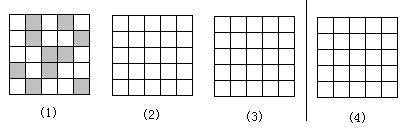
例 2、如图,先将图（1）中的图形平移到图（2）的方格中，然后绕右下角的顶点旋转180°到图（3）的方格中，再翻折到图（4）的方格中。
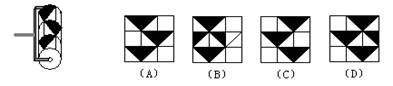
例 3、小明用如下左图的胶滚沿从左到右的方向将图案滚涂到墙上，右边所给的四个图案中符合胶滚的图案的是 （ ）
二、练习
1．下列图形不是立体图形的是 （ ）
A．球 B．圆柱 C．圆锥 D．圆
2．圆柱的侧面是 面，上、下两个底面都是 。
3．若一个棱柱的底面是一个七边形，则它的侧面必须有 个长方形，它一共有 个面。
4、想一想会不会有一个多面体，它有10个面，30条棱，20个顶点？
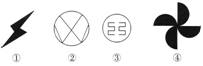5、如图所示的四个图形，既可以通过翻折变换、又可以通过旋转变换得到的图形是
（ ）A．①②③④ B．①②③ C．①③ D．③
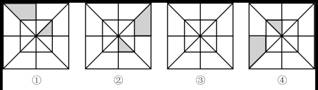6、分析图①,②,④中阴影部分的分布规律，按此规律在图③中画出其中的阴影部分。
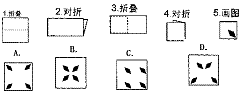7、．如果你按照下面的步骤做（如下图所示），当你完成到第五步的时候，将纸展开，会得到图形
（ ）
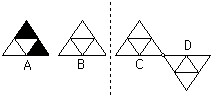
8、如图所示，按要求作图：
（1）将图形A平移到图形B；
（2）将图形B沿图中虚线翻折到图形C；
（3）将图形C沿其右下方的顶点旋转
180°到图形D。
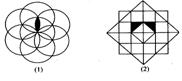
9、下面各图都是只有一条对称轴的图形，请你涂黑图形的一部分，使它成为具有两条或两条以上对称轴的图形。
10、矩形绕其一边旋转一周形成的几何体叫 ，直角三角形绕其中一条直角边旋转一周形成的几何体叫 。
11．下列现象中是平移的是 （ ）A．将一张纸沿它的中线折叠 B．飞蝶的快速转动C．电梯的上下移动D．翻开书中的每一页纸张
12、在同一平面内用游戏棒搭4个大小一样的等边三角形，至少要 根游戏棒；在空间搭4个大小一样的等边三角形，至少要 根游戏棒；
初一数学期末复习讲义 编写人：古 光
复习内容：第5章走进图形世界—展开与折叠、从三个方向看
一、知识点复习及例题选讲
1、知识点1 ：常见立体图形的展开图的识别与画出
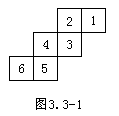
例1、如图3.3-1在正方体的展开图上编号，请写出相对面（相对面没有公共棱）的号码：1对应（ ）；2对应（ ）；3对应（ ）。
例2、下列图形是四棱柱的侧面展开图的是 （ ）
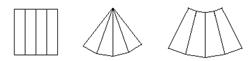
（A） （B） （C） （A） （B） （C）
例2、上列图形中为三棱柱的展开图的是 （ ）
例3、在下列图形中（每个小正方形都是相同的正方形），是正方体的表面展开图的是（ ）
（A） （B） （C） （D）
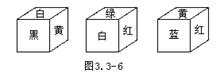
例4、如图3.3-6，下面三个正方体的六个面都按相同规律涂有红、黄、蓝、白、黑、绿六种颜色，那么涂黄色、白色、红色的对面分别是 （ ）
例5、侧面展开图是扇形的是 （ ）
A、圆柱 B、棱柱 C、圆锥 D、棱锥
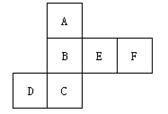
例6、如图是一个正方体的平面展开图，每个面上都标上了字母，请根据要求回答问题：（1）如果A在上面，那么哪一面会在下面？（2）如果F在上面，从右边看是E，那么哪一面会在底部？（3）如果从左边看是D，B在底部，那么哪一面会在上面？
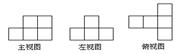
2、知识点2 ：从三个方向看，主视图：行 高 ；左视图：排 高 ；俯视图：行 排 ；
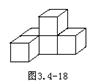
例1、如图3.4-18，是一个由五个小正方体搭成的物体，请画出它的三视图。
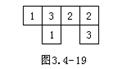
例2、如图3.4-19，是由几个小正方体木块所搭成的几何体的俯视图，小正方形中的数字表示该位置的小正方体的个数，请画出这个几何体的主视图、左视图。
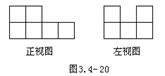
例3、在桌上摆有一些大小相同的正方体木块，正视图、左视图如图3.4-20，要摆出这样的图形至少需要 块正方体木块，至多需要 块正方体木块。
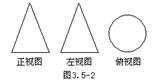
例4、如图3.5-2的三视图所画的几何体是 。
二、练习
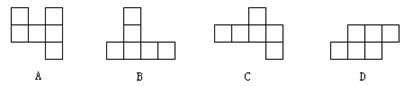
1、正方体的平面展开图可以是下列图形中的 （ ）
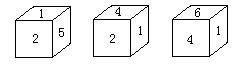2、有一块正方体木块，它的六个面上分别标上数字1~6，下图是这个正方体木块从不同面所看到的数字情况，请问5对面的数字是
（ ）A、3 B、4 C、6 D、无法确定
3、主视图、左视图和俯视图都是正方形的几何体是 。
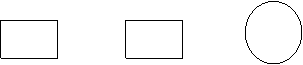4、一个立体图形的三视图形如图所示，则该立体图形是
（ ）
A、圆锥 B、球 C、圆柱 D、圆
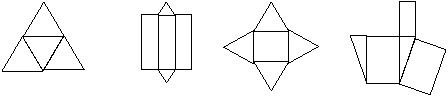
5、已知某多面体的平面展开图如图所示，
其中是三棱柱的有 （ ） 正视图 左视图 俯视图
A、1个 B、2个 C、3个 D、4个
6、如果一个立体图形的三个视图都是正方形，那么关于这个立体图形的以下三种说法正确的有 （ ）①这个立体图形是四棱柱；②这个立体图形是正方体；③这个立体图形是四棱锥； A、1个 B、2个 C、3个 D、以上全不对
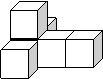
7、画出下图中由几个正方体组成的几何体的三视图。8、画出下列几何体的三视图。
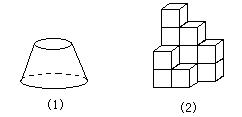
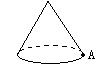
9、如下图，在圆锥的底面圆周A点处有一只蚂蚁，要从侧面爬一圈后，再回到A点，请你结合圆锥的侧面展开图，设计一条最短路线。
10、如图，是一个立体图形的三视图，这个立体图形是由一些相同的小正方体构成，这些相同的小正方体的个数是 （ ）A、4个 B、5个 C、6个 D、7个
