《平面直角坐标系》整章测试

七年级数学 第六章《平面直角坐标系》整章测试

　　一、填空题(每题4分，共32分)

1，点M(a,0)在＿＿＿轴上；点N(0,b)在＿＿＿轴上.

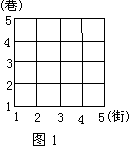
2，如图1所示,从2街4巷到4街2巷,走最短的路线的走法共有＿＿＿种.　　

3，如图2所示，进行"找宝"游戏,如果宝藏藏在(4，5)字母牌的下面, 那么应该在字母＿＿＿的下面寻找.

­　　4，点P(a，b)与点Q(a，－b)关于＿＿＿轴对称；点M(a，b)和点N(－a，b) 关于＿＿＿轴对称.

­　　5，△ABC中，A(－4,－2),B(－1,－3),C(－2,－1),将△ABC先向右平移4个单位长度,再向上平移3个单位长度,则对应点A′、B′、C′的坐标分别为＿＿＿、＿＿＿、＿＿＿.

6，已知点M(－4，2),将坐标系先向下平移3个单位长度,再向左平移3个单位长度,则点M在新坐标系内的坐标为＿＿＿.

7，如图3，直角坐标系中一条圆弧经过网格点A、B、C，其中，B点坐标为（4，4），则该圆弧所在圆的圆心坐标为＿＿＿.　

8，，观察图象，与图4中的鱼相比，图5中的鱼发生了一些变化.若图4中鱼上点P的坐标为（4，3.2），则这个点在图5中的对应点P₁的坐标为＿＿＿（图中的方格是1×1）.

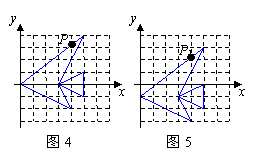　　二、选择题(每题4分，共32分)

9，点P（m +3，m +1）在直角坐标系的x轴上，则P点坐标为（　　　）

A，（0，－2）　　B，（2，0）　　C，（0，2）　　D，（0，－4）

10，在直角坐标系xOy中，已知A（2，－2），在y轴上确定点P，使△AOP为等腰三角形，则符合条件的点P共有（　　　）

A，2个　　　B，3个　　　C，4个　　　D，5个

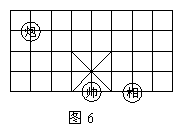
11，如图6所示的象棋盘上，若帅位于点（1，－2）上，相位于点（3，－2）上，则炮位于点　　（　）

A，（－1，1） 　　B，（－1，2）　　C，（－2，1）　　 D，（－2，2）

12，若A（a，6），B（2，a），C（0，2）三点在同一条直线上，则a的值为（ ）
　　A，4或－2　　B，4或－1　　 C，－4或1　　D，－4或2

13，已知坐标平面内三点A(5,4),B(2,4),C(4,2),那么△ABC的面积为(　 )

­　　A.3­ 　 　　 B.5­ 　　　　　C.6­ 　 　　　 D.7

­　　14，小明家的坐标为(1，2),小丽家的坐标为(－2,－1),则小明家在小丽家的(　 )

­A.东南方向­ 　　B.东北方向　　­C.西南方向　　­D.西北方向

15，已知点A（2，0）、点B（－，0）、点C（0，1），以A、B、C三点为顶点画平行四边形．则第四个顶点不可能在(　 )

A.第一象限　　　　　 　B.第二象限　　C.第三象限　　D.第四象限

­　　16，已知点A(0，－1)，M(1，2)，N(－3，0),则射线AM和射线AN组成的角的度数(　 )

­  　A.一定大于90°­　B.一定小于90°　C.一定等于90°­　 D.以上三种情况都有可能

　　三、解答题(共36分)

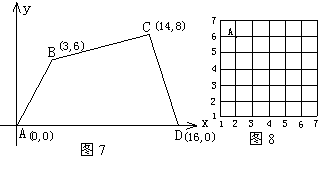
17，如图7所示的直角坐标系中,四边形ABCD各个顶点的坐标分别是A(0，0)，B(3，6)，C(14，8)，D(16，0)，确定这个四边形的面积.　

　

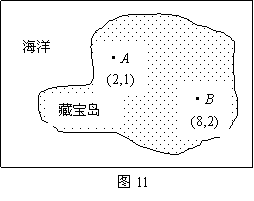
　　18，如图8所示，A的位置为(2，6)，小明从A出发,经(2,5)→(3,5)→(4,5)→(4,4)→(5,4)

→(6,4),小刚也从A出发,经(3,6)→(4,6)→(4,7)→(5,7)→(6,7),则此时两人相距几个格?

19，如果│3x+3│+│x+3y-2│=0,那么点P(x,y)在第几象限?点Q(x+1,y-1)在坐标平面内的什么位置?

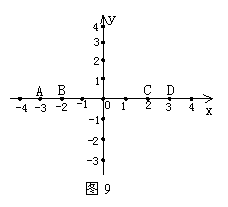
­　　20，如图9所示，C、D两点的横坐标分别为2，3,线段CD=1；B、D两点的横坐标分别为－2，3,线段BD=5；A、B两点的横坐标分别为－3,－2,线段AB=1.

­  (1)如果x轴上有两点M(x₁,0),N(x₂,0)(x₁<x₂),那么线段MN的长为多少?

­  (2)如果y轴上有两点P(0,y₁),Q(0,y₂)(y₁<y₂),那么线段PQ的长为多少?

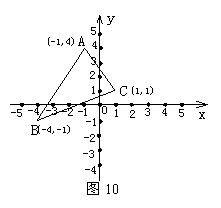21，如图10，三角形ABC中任意一点P(x₀,y₀),经平移后对称点为P₁(x₀+3,y­₀-5),将三角形作同样平移得到三角形A₁B₁C₁,求A₁、B₁、C₁ 的坐标, 并在图中画出A₁B₁C₁的位置.

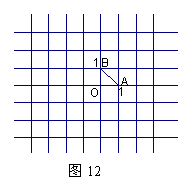
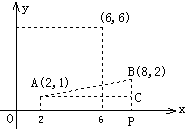
22，如图11是传说中的一个藏宝岛图,藏宝人生前用直角坐标系的方法画了这幅图,现今的寻宝人没有原来的地图,但知道在该图上有两块大石头A(2,1),B(8,2),而藏宝地的坐标是(6,6),试设法在地图上找到藏宝地点.

23，如果将点P绕定点M旋转180°后与点Q重合，那么称点P与点Q关于点M对称，定点M叫做对称中心.此时，M是线段PQ的中点.如图12，在直角坐标系中，△ABO的顶点A、B、O的坐标分别为（1，0）、（0，1）、（0，0）.点列P₁、P₂、P₃、…中的相邻两点都关于△ABO的一个顶点对称：点P₁与点P₂关于点A对称，点P₂与点P₃关于点B对称，点P₃与P₄关于点O对称，点P₄与点P₅关于点A对称，点P₅与点P₆关于点B对称，点P₆与点P₇关于点O对称，…….对称中心分别是A、B，O，A，B，O，…，且这些对称中心依次循环.已知点P₁的坐标是（1，1），试求出点P₂、P₇、P₁₀₀的坐标.

参考答案

一、1，x、y；2，6；3，X；4，x、y；5，(0，1)、 (3，0)、 (2，2)；6，(－1，5)；7，（2，0）；8，P₁（4，2.2）.

二、9，B；10，C；11，C；12，A；13，A；14，B；15，C；16，C.

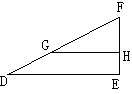
三、17，94；18，3个格；19，根据题意可得3x+3=0,x+3y-2=0,解得y=1,x=2-3y=-1,∴点P(x,y),即P(-1,1) 在第二象限,Q(x+1,y-1),即Q(0,0)在原点上；20，(1)MN=x₂-x₁　(2)PQ=y₂-y₁；21，A₁(2,-1),B₁(-1,6) C₁(4,-4)　图略；22，(1)任取1个单位长度(如1厘米),以1个单位长为直角边作直角△DEF,使DE=6个单位,EF=1个单位；(2)连结AB,以F为圆心,AB长为半径,在射线FD上截取FG=AB；(3)过点G作GH⊥FE,垂足为点H；(4)分别以A、B为圆心,GH,FH的长为半径画弧,在AB的下侧得到点C；(5)延长BC至点P,使CP=BC；(6) 过P作OX⊥BP,则OX就是X轴所在直线；(7)如图,在射线PO上截取PO=4PB,则O就是坐标原点；(8)过点O作直线OY⊥OX ；(9)以BC的长为单位长度,射线AC的方向为X 轴正方向,射线CB的方向为y轴正方向,建立直角坐标系,即可找到(6,6)的藏宝地点；毛23，P₂(1，－1) ，P₇(1，1) ，P₁₀₀(1，－3).