《三角形初步知识》练习
姓名
一、选择题
1．在下列长度的四根木棒中，能与4cm、9cm长的两根木棒钉成一个三角形的是（ ）
A. 4cm B. 5cm C. 9cm D. 13cm
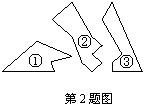
2．如图,某同学把一块三角形的玻璃打碎成三片,现在他要
到玻璃店去配一块完全一样形状的玻璃.那么最省事的办法
是带( )去配.
A. ① B. ② C. ③ D. ①和②
3．下列说法错误的是 （ ）
A. 三角形三条中线交于三角形内一点 B. 三角形三条角平分线交于三角形内一点
C. 三角形三条高交于三角形内一点 D. 三角形的中线、角平分线、高都是线段
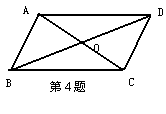4．如图,AC与BD相交于点O,已知AB=CD,AD=BC,则图中全等的三角形有（ ）
A. 1对 B. 2对 C. 3对 D. 4对
5.如图，D在AB上，E在AC上，且∠B=∠C，则下列
条件中，无法判定△ABE≌△ACD的是（ ）
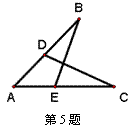A. AD=AE B. AB=AC C. BE=CD D. ∠AEB=∠ADC
6．在下列条件下，不能说明ΔABC≌ΔA′B′C′的是（ ）
A. ∠B＝∠B′，∠C＝∠C′，AB=A′B′
B. ∠A＝∠A′，∠C＝∠C′，AC=A′C′
C. ∠A＝∠A′，AB=A′B′， BC＝B′C′
D. AB=A′B′， BC＝B′C′，AC=A′C′
7．在△ABC中，若∠A＝70°－∠B，则∠C等于（ ）
A. 35° B. 70° C. 110° D. 140°
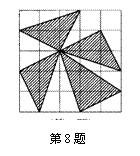
8. 如图
方格中有4个阴影三角形,其中全等的三角形（ ）
A. 有4个 B. 有3个
C. 有2个 D. 不存在
 | |||
 | |||
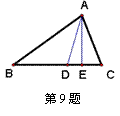9、如图，在△ABC中，AD是角平分线，AE是高，已知∠BAC=2∠B，∠B=2∠DAE，那么∠ACB为（ ）
A. 80° B. 72° C. 48° D. 36°
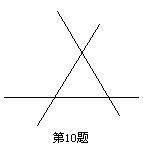
10.如图，直线表示三条相互交叉的公路，现要建一个货物中转站，要求它到三条公路的距离相等，则可供选择的地址有( )
A. 一处 B. 两处 C. 三处 D. 四处
二、填空题
11．三角形三个内角的比为2：3：4，则最大的内角是________度.
12.小华要从长度分别为5cm、6cm、11cm、16cm的四根小木棒中选出三根摆成一个三角形，那么他选的三根木棒的长度分别是:_ ， ， (单位：cm)．
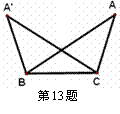
13．如图，已知AB=A′C，请问补充哪个一条件，可以得到⊿ABC≌⊿A′CB，则需补充的条件是___________ ____。（写一个即可）
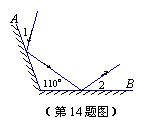
14．如图，平面镜A与B之间夹角为110°，光线经平面镜A反射到平面镜B上，再反射出去，若
，则
的度数为 ．
 | |||
 | |||
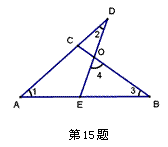
15．如图，已知∠1=42°，∠2=30°，∠3=38°，则∠4=_________。
16. ⊿ABC中，∠ABC、∠ACB的平分线相交于点O,若∠BOC = 120°，则∠A = 。
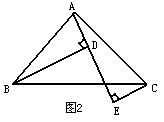
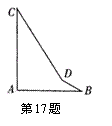
17 .一个零件形状如图所示，按规定∠A=90°，∠B=21°，
∠C=32°，才符合加工要求，检验人员测量∠BDC=143°，
则可断定这个零件 。（填“合格”或“不合格”）
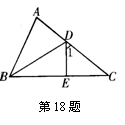
18. 如图,在⊿ABC中,已知AD=ED,AB=EB, ∠A=80O,则
∠1+∠C= 度.
 | |||
 | |||
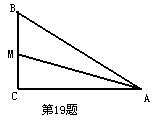
19.如图ΔABC中，∠C=90,AM平分∠CAB,CM=20cm,那么M到AB的距离是 。
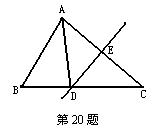
20.如图,ΔABC中,DE是AC的中垂线,AE=5cm,ΔABC的周长为30 cm,则ΔABD的周长是
三、解答题
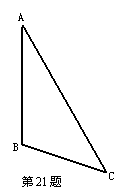
21.（8分）已知ΔABC
（1）用尺轨作出∠C的平分线和AC边上的中垂线；
（2）画出BC边上的高线和AC边上的中线.
22．（本题6分）如图，已知：A、F、C、D四点在一条直线上，AF=CD，∠D=∠A，且AB=DE．请将下面说明△ABC≌△DEF的过程和理由补充完整.
解：∵AF=CD（ ）
∴AF+FC=CD+______，即AC=DF
在△ABC和△DEF中
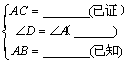
∴△ABC≌△DEF（ ）
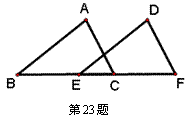
23.（本题8分）如图，B、E、C、F同在一条直线上，已知AB＝DE，BE＝CF，∠ABC＝∠DEF，试说明下列结论成立的理由：
①⊿ABC≌⊿DEF；②AC＝DF.
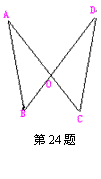
24.（本题8 分）某种产品的商标如图所示，O是线段AC、DB的交点，且AC = DB，∠A=∠D ，AB = DC，小波认为图中的两个三角形全等，他的思考过程是：
AC = DB
∠AOB = ∠DOC
△ABO≌△DCO，
AB = DC
你认为小波的思考过程正确吗？如果正确，指出他用的是
判别三角形全等的哪个条件，如果不正确，请写出一个正
确的说理过程。
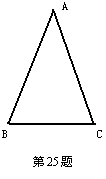25. 如右图, ⊿ABC中, ∠A=40O,∠ABC=∠ACB.AB边
的中垂线(请用圆规与直尺画出)交AC与D,交AB于
E,连结BD.
(1) 说明⊿ADE≌⊿BDE的理由;
(2) 求∠DBC的度数.(本题10分)
思考题：
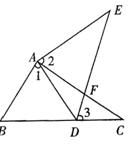
1.（10分）如图，点E在△ABC外部，点D在BC边上，DE交AC于点F，若
∠1=∠2=∠3，AC=AE，试说明：△ABC≌△ADE的理由。
2．（10分）如图，在△ABC中，∠BAC=90º，AB=AC，AE是过A的一条直线，且B，C在AE的同侧，BD⊥AE于D，CE⊥AE于E。
（１）试说明：BD+CE=DE；
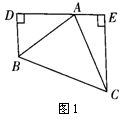（２）若直线AE绕点A旋转，使B，C在AE的异侧（如图２），其他条件不变，则BD，DE与CE的关系如何？
