《三角形的初步》训练题
班级＿＿＿＿＿ 学号＿＿＿＿＿＿ 姓名＿＿＿＿＿＿ 得分＿＿＿＿
一：选择题（30分）
1.在下列长度的四根木棒中，能与4cm，9cm长的两根木棒钉成
一个三角形的是 （ ）
A、4cm B、5cm C、9cm D、13cm
2、在△ABC中，∠A＋∠C＝∠B，那么△ABC是 （ ）
A、等边三角形 B、锐角三角形 C、钝角三角形 D、直角三角形
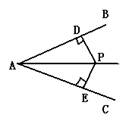
3、如图：PD⊥AB，PE⊥AC，垂足分别为D、E，
且AP平分∠BAC，则△APD≌△APE的理由是 （ ）
A、SAS B、ASA C、SSS D、AAS
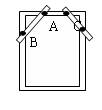4.如图，木工师傅在做完门框后，为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的AB、CD两根木条)，这样做是运用了三角形的( )
A、全等性 B、灵活性 C、稳定性 D、对称性
5.下列说法中错误的是（ ）
A、三角形三条角平分线都在三角形的内部
B、三角形三条中线都在三角形的内部
C、三角形三条高都在三角形的内部
D、三角形三条高至少有一条在三角形的内部
6.小明给小红出了这样一道题：如右图，由AB=AC，∠B=∠C，
便可知道AD=AE。这是根据什么理由得到的？小红想了想，
马上得出了正确的答案。你认为小红说的理由（ ）
A、SSS B、SAS C、ASA D、AAS
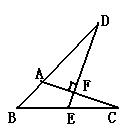
7、如图，点E在BC上，ED丄AC于F，交BA的延长线于D，已知∠D＝30°，∠C＝20°，则∠B的度数是 （ ）
A、20° B、30° C、40° D、50°
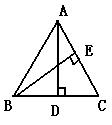8、如图，AD、BE都是△ABC的高，由与∠CBE一定相等的角是（ ）
A、∠ABE B、∠BAD C、∠DAC D、∠C
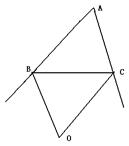9、如图，在△ABC中，∠ABC和∠ACB的外角平分线交于点O，且∠BOC＝40°，则∠A＝ （ ）
A、10° B、70° C、100° D、160°
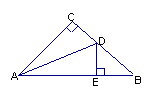10.如右图，△ABC中，∠C=90°，AC=BC，AD是∠CAB的平分线，DE⊥AB于E。已知AB=6cm，则△DEB的周长为（ ）
A、5cm B、6cm C、7cm D、8cm
二、填空题（24分）
11、直角三角形的一个锐角的是32°，则另一个锐角是＿＿＿度。
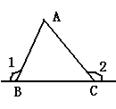
12.如图，∠A＝80°，∠2＝130°，则∠1＝＿＿＿＿度
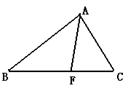13、如图△ABC中，F是BC上的一点，且CF＝BF,
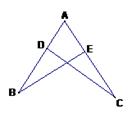那么△ABF与△ACF的面积比是＿＿＿＿＿
14、三角形的两边工分别为2cm，5cm，第三边长为xcm也是整数，则当三角形的周长取最大值时x的值为＿＿＿cm。
15.如图AB=AC，要使△ABE≌△ACD，应添加的条件是
＿＿＿＿＿＿＿＿＿(添加一个条件即可)
| |
| |
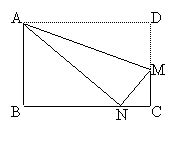
16、如图，矩形ABCD中(AD>AB)，M为CD上一点，
若沿着AM折叠，点N恰落在BC上，
∠ANB+∠MNC=____________；
17.如图，在△ABC 中，AB=AC，AB的中垂线DE交AC于点D，交AB于点E，如果BC=10，△BDC的周长为22，那么AB=
_
18、已知Rt△ABC的两直角边长分别为3cm，4cm,斜边长为5cm，则斜边上的高等于＿＿＿＿cm。
三、解答题（46分）
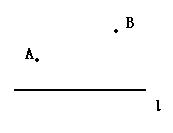19、作图题（6分）如图，点A、B是直线ｌ外不同的两点，请在直线ｌ上确定一点D，使点D到A、B的距离相等。（要求用直尺和圆规作图，保留作图痕迹，并说明结论）
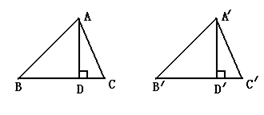
20、（10分）全等三角形对应边上的高相等，请说明理由（填空）。
已知：如图，已知△ABC≌△A/B/C/，AD⊥BC于D，A/D/⊥B/C/于D/，
请说明AD＝A/D/的理由。
解：∵△ABC≌△A/B/C/，
∴AB＝A/B/ （ ）
∠B＝∠B/ （ ）
在△ABD和△A/B/D/中
∠B＝∠B/
AB＝A/B/
∠ADB＝∠A/D/B/＝90°（ ）
∴△ABD≌△A/B/D/ （ ）
∴AD＝A/D/ （ ）
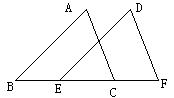21、（10分）如图，点B,E,C,F在同一条直线上，且AB＝DE，AC＝DF，
BE＝CF，则∠A＝∠D, 试说明理由。
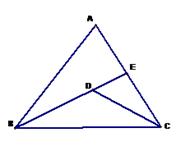22．（10分）如图在△ABC中，，D是∠ACB与∠ABC的角平分线的交点，BD的延长线交AC于E，且∠EDC=50°，求∠A的度数.
23. (10分)如图，CD⊥AB于点D，BE⊥AC于点E，BE，CD交于点O，
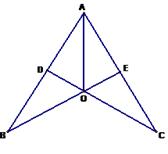且AO平分∠BAC,则OB与OC相等吗？请说明理由.