七年级数学第一学期期末考试（人教版）
一、 用心选一选（2′×8）
1、如图1，∠AOC和∠BOD都是直角，如果∠AOB＝140°，则∠DOC的度数是（ ）
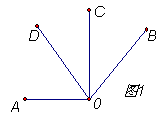A、30° B、40° C、50° D、60°
2、在下面的图形中（ ）是正方体的展开图。
 | |||||||
 |  |  | |||||
A
B
C
D
3、下列判断正确的是（ ）
A、一个数的相反数是负数 B、最大的负数是－1
C、非负数中最小数是零 D、比正数小的数都是负数
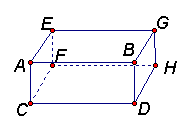
4、如图2是一个长方体，则下列说法中正确的是（ ）
A、长方体的每条棱长相等 B、与棱AC平行的棱只有2条 C、长方体的棱数是其面数的2倍 D、长方体共有4个面，8个顶点。
5、图3是一个正方体，用一个平面去截这个正方体，其截面形状不可能为下图中的（ ）
 |
6、如果3x4n－7－1＝5是关于x的一元一次方程，则n的值等于（ ）
A、2 B、3 C、4 D、6
7、我国是一个严重缺水的国家，大家应倍加珍惜水资源，节约用水。据测试，拧不紧的水龙头每秒种会滴下2滴水，每滴水约0.05毫升，小明同学在洗手后，没有把水龙头拧紧，当小明离开4小时后水龙头滴了（ ）毫升水。（用科学记数法表示）
A、1440 B、1.44×103 C、0.144×104 D、144×102
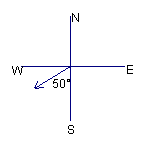
8、某测绘装置上一枚指针指向南偏西50°（如图4），把这枚指针按逆时针方向旋转1／4周，则结果指针的指向（ ）
A、南偏东50° B、西偏北50° C、南偏东40° D、东南方向
二、 静心填一填（2′×12）
1、（－1）2004＋（－1）2005＝ 。
2、一个角是60°，它的余角是 度，补角是 度。
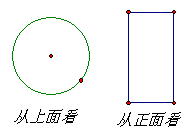3、如图5的两个图形分别是从某个几何体的上面和正面观察得到的平面图形，则该几何体是 。
4、数轴上，3和－2.5所对应的点之间的距离是 。
5、写出一个满足下列条件的一元一次方程：某个未知数的系数是1／2且方程的解为3，则这样的方程可写为 。
6、25.36°是 度 分 秒。
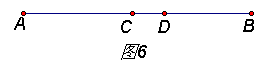
7、如图6，若C为线段AB的中点，D在线段CB上，DA＝6，DB＝4，则CD的长度是 。
8、最大的负整数与最小自然数的和是 。
9、1.0999精确到千分位的近似数是 ，此时有 个有效数字。
10、下列各数
，－1／5,0，0.3，0.2中，互为相反数的是 。互为倒数的是 。
11、2004年北京市初中毕业、升学考试各学科的满分值情况如下表：
| 科目 | 语文 | 数学 | 英语 | 社会政治 | 自然科学 | 体育 |
| 满分值 | 150 | 150 | 120 | 100 | 200 | 30 |
若把上表各学科满分的比值按比例绘成扇形统计图，则数学所在的扇形圆心角是 度。
12、某产品原价a元，第一次提价b％，第二次又降价b％，这时的价格是 元。
三、 细心算一算（5′×3）
1、11＋（－1／2）－（－7）＋（－1／6）＋（＋2）－（＋1／3）
2、 －3×［（－4）2＋2］－（－3）2÷（－2）＋（－2）3
3、11／5×（1／3－1／2）×3／11÷5／4
四、 耐心解一解（4′×2）
1、0.4（2x＋3）＝0.8（1－x）－0.5（x－2）
2、
五、 数学与生活（第1、2小题各7分，第3小题8分，共22分）
1、（7分）某商店选用两种价格分别为每千克28元和每千克20元的糖果混合成杂拌糖果后出售，为使这种杂拌糖果的售价是每千克是每千克25元，要配置这种杂拌糖果100千克，问要用这两种糖果各多少千克？（才能使混合前后销售额不变）
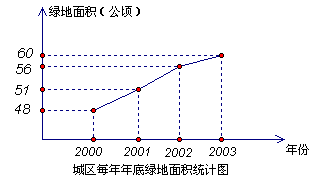
2、美化城市，改善人们的居住环境已成为城市建设的一项重要内容。某市区近几年来，通过拆迁旧房，植草、栽树、修建公园等措施，使城区绿地面积不断增加。根据图中所提供的信息，回答下列问题：
（1）2003所底的绿地面积为 公顷，比2002年底增加了 公顷；在2001年、2002年、2003年这三年中，绿地面积增加最多的是 年。（4′）
（2）为满足城市发展的需要，计划2005年底使城区绿地总面积达到72.6公顷，试求2005年底绿地面积对2003年底绿地面积对2003年底的增长率。（3′）
3、育才中学七年级学生步行到郊外支旅游，（1）班学生组成前队，步行的速度为4千米／小时，（2）班的学生组成后队，速度为6千米／小时，前队出发2小时后，后队（2）班才出发，同时各队派出一名联络员骑自行车在两队之间不间断地来回进行联络，他们骑车的速度为12千米／小时。
试根据以上的事实，提出一个问题并利用列方程的方法解决你所提出的问题（少用1个已知条件扣2分）
你提出的问题是： 。
六、 探索与猜想（第1小题4分，第2小题10分，共14分）
1、图①是一个三角形，分别连接这个三角形三边的中点得到图②；再分别连接图②中间小三角形的三边的中点，得到图③。
（1）图②有 个三角形；图③有 个三角形。
（2）按上面的方法继续下去，第n个图形中有多少个三角形？（用含有n的字母表示结论）
2、①用一根长80厘米的绳子围成一个长方形，且这个长方形的长比宽多10厘米，则这个长方形的长和宽是多少？这个长方形的面积是多少？
②有这根绳子围成一个正方形，则这个正方形的垞是多少、面积是多少？
③如果用这根绳子围成一个圆，则这个圆的半径是多少？面积是多少？
④比较上面的①②③运算所得出的结果，你能获得什么猜想？