七年级数学检测
一、填空题
1、如果四边形有一个是直角，另外三个角的度数之比为2：3：4，那么这三个内角度数分别为
。
2、n边形内角和为 ，十边形内角和为 。
3、相同正多边形铺满地面的条件是设其边数为 。
4、在正多边形中能够铺满地面的是 （正方形、正多边形、正八边形、正六边形）
5、多边形的每个外角都是相邻内角的，则此多边形的边数是 ，内角和是 ，外角和是 。
6、多边形每一个内角都等于150°，则从此多边形一个顶点出发的对角线有 条，一共有
条对角线。
7、一个多边形的内角和与外角和为2160°，这个多边形的边数为 。
8、一个多边形中，它的内角最多可以有 个锐角。
9、如果一个正多边形的每个内角都等于156°，则这个多边形是 边形。
10、为什么桥梁拉杆、电视塔底座是三角形的结构，而不是四边形、五边形结构，是因为 。
二、选择题
11、有关正多边形的意义正确的是············································································ （ ）
（A）多边形的各边都相等，个内角都相等，那么它为正多边形
（B）五边形是正五边形
（C）每条边都相等的四边形都是正多边形
（D）以上都不对
12、已知一个多边形内角和是2340°，则这个多边形的边数是···································· （ ）
（A）13边 （B）15边 （C）16边 （D）以上都不对
13、在①正三角形、②正方形、③正六边形中能密铺平面的是·································· （ ）
（A）①②③ （B）②③ （C）①③ （D）以上都不对
14、下列正多边形的组合中，能铺满地面的是··························································· （ ）
（A）正八边形和正方形 （B）正五边形和正八边形
（C）正六边形和正三角形 （D）正五边形和正三角形
15、（n＋1）边形的内角和比n边形的内角和大························································· （ ）
（A）180° （B）360° （C）n·180° （D）n·360°
16、一个多边形的内角和是它的外角和的3倍，则这个多边形是（ ）边形
（A）6 （B）7 （C）8 （D）9
17、下列能密铺平面的是·························································································· （ ）
①正六边形和三角形 ②正十二边形和正三角形 ③正八边形和正方形 ④正方形和正三角形
（A）①②③ （B）②③④ （C）②③ （D）①②③④
18、一个多边形除了一个内角外，其余内角和为2570°，则这一个内角等于··············· （ ）
（A）90° （B）105° （C）130° （D）120°
三、解答题
19、求下列正多边形的内角和的度数
（1）五边形 （2）八边形 （3）十二边形
20、在各个内角都相等的多边形中，一个外角等于一个内角的，求这个多边形的每一个内角的度数和它的边数。
21、一个多边形中各内角相等，且每个内角和外角之差的绝对值为60°，求这个多边形的边数。
22、一个正多边形的一个内角与相邻外角之比为3：2，求这个多边形的内角和。
23、某多边形的所有内角与某一个外角总和为1340°，你知道它是几边形？这个外角是多少？
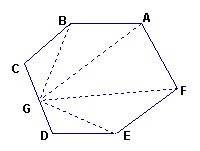
24、如图在六边形ABCDEF中，G是CD上一点,连BG、GE、FG、AG
（1）你能通过三角形的内角和定理计算出六边形内角和是多少吗?
（2）由此能推出n边形的内角和吗?画图说明
.
25、请化出正方形,正六边形,正十二边形铺满地面的图形
26、某单位的地板由三种正多边形的小木板铺成，设这三种多边形的边数分别为x、y、z，求＋＋的值。