七年级（上）数学期中复习题（一）
（华师大版）
（满分100分，时间100分钟）
一、选择题（每小题3分，满分30分）
本题共有10小题，每一个小题都给出代号为A、B、C、D的四个结论，其中只有一个结论是正确的，把你认为正确结论的代号写在该题后的括号内，每小题选对得3分，不选、选错或者选出的代号超过一个，一律得0分。
（1）下列计算中，不正确的是（ ）
（A）（-6）+（-4）=2 （B）-9-（-4）=-5 （C）∣-9∣+4=13 （D）-9-4=-13
（2）下列交换加数位置的变形中，正确的是（ ）
（A）1-4+5-4=1-4+4-5 （B）1-2+3-4=2-1+4-3
（C）4.5-1.7-2.5+1.8=4.5-2.5+1.8-1.7 （D）-
+
-
-
=+--
（3）近似数2.30×104的有效数字有（ ）
（A）5个 （B）3个 （C）2个 （D）以上都不对
（4）-，-
，-
的大小顺序是（ ）
（A）-<-<- （B）-<-<- （C）-<-<-
（D）-<-<-
（5）如果a表示有理数，那么下列说法中正确的是（ ）
（A）+a和-（-a）互为相反数 （B）+a和-a一定不相等
（C）-a一定是负数 （D）-（+a）和+（-a）一定相等
（6）对于多项式22m2+3m-1，下列说法正确的是（ ）
（A）它是关于m的四次三项式 （B）它的常数项是1
（C）它是按m降幂排列 （D）它是按m升幂排列
（7）算式（-3）×4可以化为（ ）
（A）-3×4-×4 （B）-3×4+3 （C）-3×4+×4 （D）-3×3-3
（8）某宾馆的标准间每个床位标价为m元，旅游旺季时上浮x%，则旅游旺季时标准间的床位价为（ ）
（A）m·x%（元） （B）m+ x%（元） （C）m（1+ x%）（元） （D）m（1- x%）（元）
（9）如图，在数轴上有a、b两个有理数，则下列结论中，不正确的是（ ）
（A）a+b<0 （B）a-b<0
（C）a·b<0 （D）（-
）3>0
（10）如果∣a+2∣+（b-1）2=0，那么代数式（a+b）2001的值是（ ）
（A）-2001 （B）2001 （C）-1 （D）1
二、填空题（每小题3分，满分30分）
（11）水位上升20cm记作+20cm，-15cm表示______________________。
（12）-3的相反数是___________；倒数是____________；-32=___________。
（13）（-4）+（-3）-（-2）-（+1）省略加号的和的形式是________________________。
（14）在月球表面，白天，阳光垂直照射的地方温度高达+127℃；夜晚，温度可降低到-183℃。则月球表面昼夜的温差为____________。
（15）根据要求，用四舍五入法取下列各数的近似值：
1.4249≈______（精确到百分位）；0.02951≈________（精确到0.001）。
（16）观察下面的一列数，按某种规律在横线上填上适当的数：
1，-2，4，-8，________，_______。
（17）月球轨道呈椭圆形，近地点平均距离为363300千米；远地点平均距离为405500千米。用科学记数法表示：近地点平均距离为___________________________；远地点平均距离为___________________________。
（18）当x=-1时，代数式x3-x2+x+1的值是___________。
（19）在一次募捐活动中，平均每名同学捐款a元，结果一共捐了b元，则式子
可解释为：_________________________________________________
（20）某地出租车收费标准为：起步价5元，3千米后每千米1.4元，某人乘坐出租车5千米，应付费_________元；乘坐x（x>3）千米，应付费__________元。
三、解答题（每小题4分，满分20分）
（21）根据下面给出的数轴，解答下面的问题：
（1）A、B两点之间的距离是多少？
（2）画出与点A的距离为2的点（用不同于A、B的字母表示），并写出此点表示的数。
（22）计算：（+4.3）－（－4）+（－2.3）－（+4）
（23）计算：（－48）÷6－（－25）×（-4）+8
（24）计算：8-2×32+（-2×3）2
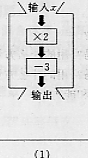
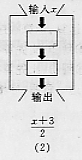（25）下面是一组数值转换机，写出图（1）的输出结果；找出图（2）的转换步骤（填写在框内）
四、解答题（每小题5分，满分10分）
（26）计算：－4－[－5+（0.2×-1）÷（-1
）]
（27）当a=－1，b=－
，c=1时，求代数式b2-4ac的值，并指出求得的这个值是哪些数的平方。
五、探究题（满分10分）
（28）观察、分析下面两个例题的计算方法：
例1 计算：（1－-
）÷（-）+（-2）÷
解：原式=（1--）×（-
）+（-2）÷
①
=
×（-）+（-）×（-）+（
）×（-）+（-2）×
②
=-2+1+
-
=-3
例2 计算：-1-[1-（1-0.5×）] ×[2-（-3）2]
解：原式=-1-[1-（1-）] ×（2-9）
③
=-1-（1-1+）×（2-9）
④
=-1-×（-7）=-1+
=
请回答以下问题：
（1）有理数的混合运算，运算顺序是如何规定的？
（2）例1中，步骤①到②，比先算括号里的简便吗？用的什么方法？
（3）例2中，步骤③到④，比先算括号里的简便吗？用的什么方法？
（4）学完“有理数”这一章后，你增长了哪些知识和能力？
参考答案
1.A
2.C 3.B 4.A
5.D 6.C 7.A
8.C 9.B 10.C 11.水位下降15cm 12. 3；；-9
13．-4-3+2-1 14. 310℃ 15. 1.42；0.030 16. 16；-32 17. 3.633×105千米；4.055×105千米 18. -2 19. 共有名同学参加捐款（或：b除以a的商） 20. 7.8；5+1.4(x-3)(x>3)
21. （1）1.5-（-2.5）=4 （2分）
（2）这样的点共有两个：C表示3.5，D表示-0.5 （2分）
22．原式=[（+4.3）+（-2.3）]+[-（-4）-（+4）] （1分）
=（+2）+0 （2分）
=2 （1分）
23．原式=（-8）-（+100）+8 （2分）
=-100 （2分）
24．原式=8-2×32+（-6）2 （1分）
=8-18+36 （2分）
=26 （1分）
25．（1）输出为：2x-3 （2分）
（2）自上而下为：+3；÷2 （2分）
26．原式=-4－[-5+（
-1）÷（-
）]
（1分）
=-4-[-5+（-
）×（-
）]
（1分）
=-4-（-5+）
（1分）
=-4+5-
（1分）
=
（1分）
27．当a=-1，b=-，c=1时，
b2-4ac=（-）2 -4×（-1）×1
（1分）
=+4×1×
（2分）
=
（1分）
是+
或-的平方
（1分）
28．（1）有理数的混合运算的顺序是： （2分）
1．先算乘方，再算乘除，最后算加减；
2．同级运算，按照从左至右的顺序进行；
3．如果有括号，就先算小括号里的，再算中括号里的，然后算大括号里的。
（2）例1中，步骤①到②，比先算括号里的简便；用的是分配律 （2分）
（3）例2中，步骤③到④，比先算括号里的简便；
用的是“减去一个数，等于加上它的相反数” （2分）
（4）略 （4分）
本题评分原则：根据学生回答的情况，结合该生平时学习过程中的表现（参与学习活动的情感、态度；自主探索、与他人合作交流的程度；作业、检测的效果；本阶段学习的变化、发展水平等）评分。