初一数学第一学期期末考试1
一、填空(每空2分，共30分)
1．已知 a＋1 ＋(b－2)2＝0，那么a b＝________．
2．已知有理数a、b、c在数轴上位置如图所示，那么化简代数式 a＋b
－ a－c ＋ b＋c － c－b 得_________．
3．将一张厚度为a毫米的白纸对折32次，其厚度为_________________毫米(只要求列出计算式子，不要求计算出结果)．
4．当x＝2时，ax5＋bx3＋cx－5＝5，则当x＝－2时，ax5＋bx3＋cx－5＝_____．
5．观察下列等式：4－1＝3，9－4＝5，16－9＝7，25－16＝9，……，请将你所发现的规律用含有n (n为正整数)的等式表示出来，则为____________．
6．如图，设图中一共有a条直线，一共有b条射线，一共有c条线段，则代数式a＋b＋c的值等于__________．
7．若∠1与∠2互余，∠2与∠3互补，且∠1＝63º，则∠3＝________．
8．如图，∠BAC＝∠ACD，则∠BCD＋∠________＝180º．
 |
(第6题) (第8题) (第9题)
9．如图，若∠ABC＝30º∠CBD＝70º，BE平分∠ABD，则∠DBE＝______º．
10．下面给出三件事情：(1) 一个有理数的平方是正数；(2) 一个有理数的平方是负数；(3) 一个锐角的补角比它的余角大90度．在这些事情中，可能的事情是______________(填序号)．
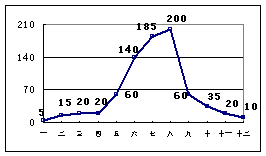11．如图，这是我国某市一年的降水量统计图(单位：毫米)，观察并回答：
(1) ______月份的降水量最大，____月份的降水量最小；
(2) 此城市年总降水量_____毫米；
(3) 该城市在我国____部(东或西)．
12．There is a group of numbers: 5, 8, 11, 5, 7, 8, 9, 5, 12, 10, 3, 15.
Then the relative frequency of 5 is__________.
二、选择题(每题2分，共20分)
13．在
ab，
，
，1，
中，单项式有( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
14．有理数a、b满足a＝2003b，则( )
(A) a≥b (B) a ≤b (C) a≥ b (D) a ≥ b
15．下列式子正确的是( )
(A) x－(y－z)＝x－y－z (B) －(x－y＋z)＝－x－y－z
(C) x＋2y－2z＝x－2(y＋z) (D) －a＋c＋d＋b＝－(a－b)－(－c－d)
16．下列的4个图形中能够经过折叠后围成一个正方体的是(
)
(A) (B) (C) (D)
17．下列说法：(1) 两点之间的距离就是连结这两点的线段
(2) 与同一条直线垂直的两条直线也垂直
(3) 一个锐角的补角比这个锐角的余角大90度
(4) 同位角相等，两直线平行
其中正确的有( )
(A) 1个 (B) 2个 (C) 3个 (D) 4个
18．如图所示，这个几何体的三视图正确的是( )
(A) (B) (C) (D)
19．如图，由A点测B点的方向是( )
(A) 南偏东30º (B) 南偏东60º
(C) 北偏东30º (D) 北偏西60º
20．下面事情中必然发生的是( )
(A) 今天是星期一，昨天是星期二 (B) 明天会下雨
(C) 小明数学考试得99分 (D) 明年有366天
21．如图，AB∥CD∥PQ，若∠ABC＝50，
∠CPQ＝150º，则∠BCP等于( )
(A) 60º (B) 50º (C) 30º (D) 20º
22．In the picture,if ∠AOB＝90º ,OD is the angular bisector of ∠BOC and OE is the angular
bisector of ∠AOC, then ∠EOD＝( )
(A) 30º (B) 45º (C) 50º (D) 60º
三、解答题
23．－42－(－4)2 (5分)
24．
(5分)
25．已知A＝3x＋2y2，B＝x2―2x―y2，且x＝2， y－1 ＝3，试求A＋B的值．(5分)
26．已知a2－ab＝2，4ab－3b2＝－3，求代数式a2－13ab＋9b2－5的值．(5分)
27．如图，直线AB、CD相交于点O，OE平分∠BOC，∠AOE＝115º，请你把求∠AOD的推理过程补充完整．(5分)
解 ∵ AOB是一条直线(已知)
∴ ∠AOE＋∠BOE＝180º(平角定义)
∵ ∠AOE＝115º(已知)
∴ ∠BOE＝_________º(等式性质)
∵ OE平分∠BOC(已知)
∴ ∠BOC＝2∠BOE(角平分线定义)
∴ ∠BOC＝_________º
∵ 直线AB、CD相交于点O(已知)
∴ ∠AOD与∠BOC是对顶角(对顶角定义)
故 ∠AOD＝∠BOC(______________)
∴ ∠AOD＝__________º(____________)
28．已知：如图，F、E分别在AB、CD的延长线上，AF∥CE，∠A＝∠C，EF分别交AD、BC于点G、H．
求证：∠AGF＝∠CHE．(5分)
29．某班全体同学在“献爱心”活动中都捐了图书，捐书情况如下表所示：
| 每人捐书的册数 | 5 | 10 | 15 | 20 |
| 相应的捐书人数 | 17 | 22 | 4 | 2 |
请根据题目中所给出的条件回答下列问题：
(1) 该班共有学生__________名．
(2) 全班一共捐书__________册．
(3) 若该班所捐的图书拟按右图所示的比例分送给山区学校、本市兄弟学校和本校其他班级，则送给山区学校的书比送给本市兄弟学校的书多多少册？(8分)
30．小魏驾驶汽车在公路上匀速行驶，他看到的里程碑上的数是一个两位数，一小时后看到的里程碑上的数恰好是他第一次看到的数颠倒了顺序的两位数；再过了一个小时后，小魏第三次看到的里程碑上的数又恰好是第一次看到的两位数字之间添加上了一个0之后所成的一个三位数．试问：小魏所看到的这三块里程碑上的数分别是多少？(4分)
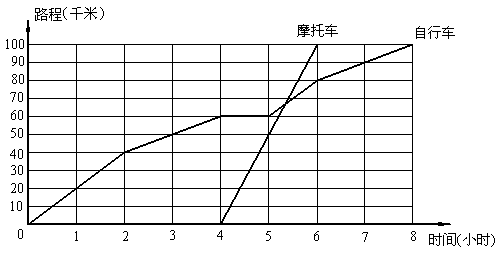
31．甲、乙两人(甲骑自行车，乙骑摩托车)从A城出发到B城旅行．如图表示两人离开A城的路程与时间之间的关系．根据图象你能够得到关于甲、乙两人旅行的哪些信息？(8分)
答题要求：(1) 请至少提供4条信息．例如甲比乙早出发4小时(或者乙比甲晚出发4小时)．
(2) 请不要再提供(1)中已经列举的信息．
 |
参考答案
一、填空
1．1 2. －b－3c 3. 232a 4.－15 5.略 6. 略 7. 153°
8. ABC 9. 50° 10. (1) 11. (1) 八，一 （2）770 （3）东 12. 25%
二、选择
13.C 14.D 15.D 16.C 17.B 18.D 19.B 20.D 21.D 22.B
三、解答题
23.－32 24.=x+2.5
25．如果y=－2,则A+B
=3×2×（－2）+2x(－2)2+22－2×2×(－2)－(－2)2
=－12+8+4+8－4
=4
如果y=4,则A+B
=3×2×4+2×42+22－2×2×4－42
=24+32+4－16－16
=28
26． 原式=(a2－ab)－(12ab－9b2)－5
=2+9－5
=6
27．65 130 对顶角相等 130 等量代换
27．解∵AF∥CE，（已知）
∴∠FAD+∠ADC=180°（两直线平行，同旁内角互补）
∵∠A=∠C（已知）
∴∠C+∠ADC=180°
∴AD∥BC（同旁内角互补，两直线平行）
∵AD∥BC
∴∠AGF=∠CHE（两直线平行，内错角相等）
29．（1）45 （2）405 （3）162册
30．（1）16 （2）61 （3）106
31．解我获得了这些信息
（1）乙骑摩托车每小时行50千米
（2）甲在途中停了一小时，说明休息了一小时
（3）甲前两个小时和信息后的第一个小时每小时行20千米
（4）乙共花了两个小时，甲共花了八个小时
（5）乙比甲一共少花六小时
（6）乙比甲早到2小时