[文件] sxtbc1jd0018.doc
[科目] 数学
[年级] 初一
[类型] 同步
[关键词] 期末
[标题] 初一期末复习试卷
[内容]
初一数学期末复习试卷
| 题号 | 一 | 二 | 三 | 四 | 五 | 六 | 总分 |
| 得分 |
一、填空（每小题3分，共30分）
1．计算
________。
2．计算
_________。
3．
。
4．
_________。
5．计算
_________。
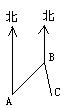
6．如图，一艘船从A点出发，沿东北方向航行至B点，再从B点出发沿南偏东15°方向航行至C点，则∠ABC等于________
 |
7．已知∠α=48°21’，则∠α的余角等于________。
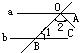
8．如图，a∥b，OC平分∠AOB，∠1=30°，则∠2=_______。
 |
9．“相等的角是对顶角”是______命题。
10．钟表上的分针走12分钟时，时针转了_______°。
二、选择题（每小题2分，共20分）
1．在下列计算中，①
②
③
④
⑤
正确的是（ ）
A、③④ B、②④ C、①③ D、②⑤
2．如果
的展开式中不含
项，则
的值为（ ）
A、2 B、—2 C、0 D、3
3．一个角的余角是它的补角的
，则这个角为（ ）
A、22.5° B、50° C、45° D、135°
4．如果二次三项式
是一个完全平方式，那么
的值是（ ）
A、9 B、3 C、—3 D、+3或—3
5．计算
等于（ ）
A、
B、
C、
D、
6．计算
得（ ）
A、
B、
C、
D、
7．下列语句中，正确的语句共有（ ）
①两点确定一条直线。②两点之间线段最短。
③两条直线相交，只有一个交点。
④将一条线段分成相等线段的点，叫做线段的中点。
A、1个 B、2个 C、3个 D、4个
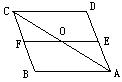8．如图，AB∥CD∥EF，BC∥AD，AC平分∠BAD，则与∠AOE相等的角有（ ）
A、2个 B、3个 C、4个 D、5个
9．下列命题是真命题的是（ ）
A．经过一点有且只有一条直线与这条直线平行
B．同位角相等
C．不相交的两条直线是平行线
D．平面内垂直于同一条直线的两条直线平行
10．如果在一条直线上得到6条不同的线段，那么在这条直线上至少要选用（ ）个不同的点。
A、12 B、6 C、5 D、4
三、解答题（每小题5分，共20分）
1．计算(x2+4y2)2+(x－2y) (2y－x) (x+2y)2
2．计算(x2+x－6) (x2－x－6) （用公式计算）
3．应用公式计算598×602
4．证明(a－1) (a2－3) + a2(a+1)－2 (a3－2a)—4－a的值与a无关。
四、解答题（每小题6分，共12分）
1．如图，OB平分∠COD，∠AOB=90°，∠AOC=125°，求比∠COD的补角小19°3′59″的角的度数。
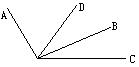
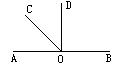2．如图，O为直线AB上一点，∠AOC=∠BOC，OC是∠AOD的平分线，求①∠COD的度数。
②判断OD与AB的位置关系。
五、（8分）已知：如图，a⊥b，b⊥c，c⊥d，求证：a⊥d。
证明：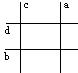
六、如图，已知AB∥CD，AE平分∠BAC，CE平分∠ACD。求证：AE⊥CE。
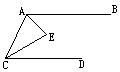（10分）
参考答案
（整式的乘除、相交线平行线综合测试）
一、1．—a5 2．x4－8x3+4x2 3．1－x 4．a4－
a2+
5．64xn+3yn 6．60° 7．41°39′ 8．75° 9．假
10．6
二、
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| A | A | C | D | B | B | C | D | D | D |
三、1．
解：原式= (x2+4y2)2－(x－2y)2 (x+2y)2 1分
= (x2+4y2)2－(x2－4y2)2 2分
= (x2+4y2+x2－4y2) (x2+4y2－x2+4y2) 3分
= 2x2·8y2 4分
=16x2y2 5分
（也可按完全平方公式展计算）
2．解：原式=[(x2－6)+x][(x2－6)－x] 1分
= (x2－6)2－x2 2分
=x4－12x2+36－x2 4分
=x4－13x2+36 5分
3．解：原式= (600－2) (600+2) 2分
=6002－22 3分
=360000—4 4分
=359996 5分
4．证明：
(a－1) (a2－3)+a2(a+1)－2 (a3－2a－4)－a
= a3－3a－a2+3+a3+a2－2a3+4a+8－a 2分
= (a3+a3－2a3)+(－a2+a2)+(－3a+4a－a)
=0 4分
∴原式的值与a的值无关。
四、1．解：∵∠AOB=90°，∠AOC=125°（已知）
∴∠BOC=∠AOC－∠AOB
=125°－90°
=35° 1分
又∵OB平分∠COD
∴∠DOC=2∠BOC
=2×35°
=70° 3分
180°－∠DOC－19°3′59″
=180°－70°－19°3′59″
=90°56′1″ 5分
答：比∠COD的补角小19°3′59″的角的度数是90°56′1″。 6分
2．解：
①∵∠AOC=∠BOC
∠AOC+∠BOC=180°
∴∠BOC+∠BOC=180°
∴∠BOC=135°
∴∠AOC=×135°= 45°
∵OC平分∠AOD （已知）
∴∠COD=∠AOC= 45°（角平分线定义）
答：∠COD的度数是45° 3分
②由①知∠AOC=∠DOC= 45°（已求）
∴∠AOD=∠AOC+∠DOC=90°
∴OD⊥AB（垂直定义） 6分
五、证明：
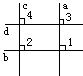
∵a⊥b，c⊥d （已知）
∴∠1=∠2=90° （垂直定义） 2分
∴a∥c（同位角相等，两直线平行）
∴∠3=∠4（两直线平等同位角相等） 5分
又∵c⊥d （已知）
∴∠4=90° （垂直定义）
∴∠3=90° 7分
∴a⊥d （垂直定义） 8分
六、证明：
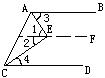
过点E作EF∥AB（平行公理） 1分
∴AB∥CD （已知）
∴EF∥CD （如果两条直线都与第三条直线平行，
那么这两条直线也互相平行）
∴∠1=∠3，∠2=∠4 5分
（两直线平行内错角相等）
又∵AE、CE分别平分∠BAC、∠ACD （已知）
∴∠3=∠BAC，∠4=∠ACD（角平分线定义） 8分
∵AB∥CD （已知）
∴∠BAC+∠ACD=180°（两直线平行，同旁内角互补）
∴∠BAC+∠ACD=90°
∴∠3+∠4=90° 12分
∴∠1+∠2=90°
∴AE⊥CE （垂直定义） 12分