初一上学期竞赛数学试题

初一上学期竞赛数学试题

（时间为70分钟，满分为120分）

一．看谁的命中率高（本题有12小题，共48分）．

1．“两点确定一条直线”，若平面内有四个点，可以确定的直线条数为（　　　）．

　  （A）1条或6条　 （B）4条或6条　 （C）1条或4条　（D）1条或4条或6条

2．如图1是一个长方体，则下列说法中正确的是（　　　）．　　　　　　　 

（A）长方体的每条棱长相等

　（B）与棱平行的棱只有2条　　

（C）长方体的棱数是其面数的2倍

（D）点到所在直线的距离是线段

3．下列调查中，调查方式选择正确的是（　　　 ）．

（A）为了了解100个灯泡的使用寿命，选择全面调查

（B）为了了解某公园全年的游客流量，选择抽样调查

（C）为了了解生产的50枚炮弹的杀伤半径，选择全面调查

（D）为了了解一批袋装食品是否含有防腐剂，选择全面调查

4．在6点10分的时候钟表上的时针和分针的夹角为（　　　）．　　　　　　　 

（A）120⁰（B）125⁰  （C）130⁰ （D）135⁰

 5．下列叙述中，正确的共有（　　　）．

（1）一个角的补角比这个角的余角大90⁰

（2）互余的两个角的比是4：6，这两个角分别是40⁰和60⁰

（3）两个角若互补，其中一个角是锐角另一个角为钝角

（4）小于平角的角是钝角

（A）0个　 （B）1个　  （C）2个　　　 （D）3个　　　 　　　　　　　

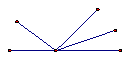
 6．如图，小于平角的角有（　　　 ）　　　　　　　　　　　　　　　　　　　

　　 （A）10个　　　(B)9个　　  (C)8个　　 (D)4个

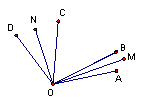 7．如图，OB,OC是∠AOD的任意两条射线，OM平分∠AOB,ON平分∠COD,若∠MON=，∠COB=,则∠AOD等于（　　　 ）．

（A）2—　 （B）— 　 （C）+ 　 （D）以上都不对

8．从A地到C地，可供选择的方案是走水路、走陆路、走空中。从A地到B地有2条水路、2条陆路，从B地到C地由条陆路可供选择，走空中，

从A地不经过B地直接到C地。则从A地到C地可供选择的方案有（　 　　）　　　　　　　　　　　 

（A）20种　　（B）8种　　（C）5种　　（D）13种　　　　　　　　　　　　　　　

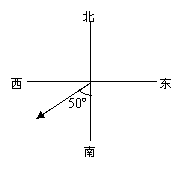9．某测绘装置上一枚指针原来指向南偏西50⁰（如图2），把这枚指针按逆时针方向旋转周，则结果指针的指向（　　　 ）．

（A）南偏东50º　（B）西偏北50º （C）南偏东40º　（D）东南方向

10．如图，在的正方形网格中，的

大小关系是（　　　）．

（A）　　　　 （B）

（C）　　　　 （D）

11.下列说法中错误的是（　　　）

（A）若B为线段AC的中点，则BC=AC

（B）若AO=BO，则O点是线段AB的中点

（C）若AO=BO=AB，则O点是线段AB的中点

（D）若OC平分∠AOB，则∠AOC=∠BOC=∠AOB

12.  某公司员工分别住在A区，B区，C区三个生活区，A区有30人，B区有15人，C区有10人，三个区在同一条直线上，位置如图所示.该公司的接送车打算在此间只设一个停靠点，为使所有员工步行到停靠点的路程之和最小，那么停靠点的位置应设在（　　　）

（A）A区　 （B）B区　 （C）C区　　（D）A、B两区之间　

二．基本知识与基本技能（本题有4小题，共28分）．

南

南

南

13．某商场在“十一”长假期间平均每天的营业额是15万元，由此推断10月份的总营业额约为15×31=465（万元 ），你认为这样的推断是否合理________，

理由是　　　　　　　　　　　  　　　　　　　 ．

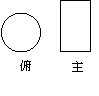
14．如图，两个图形分别是某个几何体的俯视图和主视图，则该几何体是________．

15．两个互为余角的差是20⁰，则这两个角中较小的那个角的补角是 　　　　度

16．如图，若点、D为线段上的点， cm，BC=5cm，AB=8cm,

则线段的长是________．

17．乘火车从A站出发，沿途经过3个车站方可到达B站，那么在A、B两站之间需要

安排　　　　种不同的车票．

18.如图，

 　　　= 　　 （理由：　　　　　　　　　  ）

19．2004年日照市初中毕业、升学考试各学科及满分值情况如下表：

　

科  目	语文	数学	英语	理化生	史地政
满分值	120	120	120	160	130

若把2004年日照市初中毕业、升学考试各学科满分值比例绘成扇形统计图，则数学所在的扇形的圆心角是_________度．（精确到1度）

三．计算能手　　　看谁既快又准确．

20．（本题7分）计算：（90⁰–78⁰19^/40^//）÷2

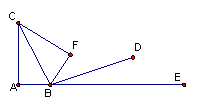
21 （本题10分）将书页一角折叠使角的顶点A落在F处，BC为折痕，BD平分∠FBE,

求∠CBD的度数

　　　　　　　　　　　　　　　　　　　　　　　　　 

22．（本题10分） 在一条直线上任取一点A，截取AB=12厘米，再截取AC=38厘米，D,E分别是AB,AC的中点，（自己画图，写步骤）

(1)求线段BC的长，　　　　　　　　　　　　　  （2）求D、 E两点之间的距离

四．数学与我们的生活

23. （本题10分）小明对我市2000年至2002年快餐公司发展情况进行调查，制成了我市快餐公司个数的条形统计图（如图甲）和快餐公司盒饭年销售量的平均数情况条形图（如图乙），利用甲、乙图共同提供的信息，解答下列问题

（1）求我市2000年销售盒饭是多少？

 (2) 我市盒饭量最大的年份是哪一年，这一年销售量是多少万盒？

（3）这三年中我市每年平均销售盒饭量是多少？

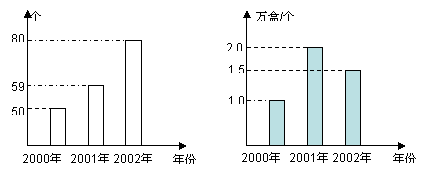
五.探索与发现

24. （本题7分）根据题意，完成下列填空

如图所示，l₁与l₂是同一平面内的两条相交直线，它们有1个交点。如果在这个平面内再画第3条直线l₃，那么这三条直线最多可有　　　个交点；如果在这个平面内再画第4条直线l4，那么这四条直线最多可有　　　　个交点；由此我们可以猜想：在同一平面内，6条直线最多可以有　　　　  个交点，n(n为大于1的整数)条直线最多可有　　　　 个交点（用含n的式子表示）