七年级（上）数学试题（一）
班级 姓名 学号
一、填空题（每小题2分，共24分）
1、比–3小5的数是 ，比–5小–7的数是 ，比0小-5的数是 .
2、已知点A在数轴上表示的数是-2，B在数轴上，AB=3，则B点所表示的数是_______。
3、如果
，那么
；
4、比较大小：
_____
.
5、船在静水中的速度为
千米/时，水流的速度为2千米/时，若A、B 两
地之间相距600千米，那么船在顺水情况下走完全程需要 小时；船在逆水情况下走完全程需要 小时；
6、48°56′47″的余角是 ，补角是 。
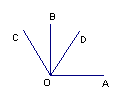
7、如图，∠AOB=90°，∠BOC＝40°，OD平分∠AOC，则∠BOD＝ °
8、时钟指向5：30，则时针与分针所成较小的那个角的度数为_________ 度.
9、教室里一般都装日光灯来照明，已知每根灯管每小时的平均耗电量约为0.04千瓦·时（俗称为度）；而1度电（1千瓦·时）价格是0.75元；设教室每天平均开灯10小时，请计算并回答以下问题：
（1）若每所中小学平均有30间教室，每间教室配有12根灯管，那么一所中小学所有教室一天的耗电量是_____________千瓦·时；
（2我市约有500所中小学；一年若按210个工作日（即上学时间）计，则每年全市中小学所有教室的照明电费约为_______________________元.
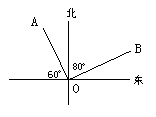10、如图OA的方向是
，OB的方向是
11、某校初中三年级共有学生400人,为了了解这些学生的视力情况,抽查20名学生的视力,对所得数据进行整理.在得到的条形统计图中, 各小组的百分比之和等于_______,若某一小组的人数为4人,则该小组的百分比为_________.
12、从鱼池中不同地方抽出30条鱼作上记号放回鱼池，一段时间 后，再捞出50条鱼其中有两条有记号，估记鱼池鱼的数目约为 。
二、选择题（每小题2分，共24分）
1、有下面的算式：①(-1)2003=-2003；②0-(-1)=1；③-
+
=-
；④
=-1；
⑤2×(-3)2=36；⑥-3÷×2=-3，其中正确算式的个数是（ ）
A、1个 B、2个 C、3个 D、4个
2、陈新的父亲到银行存入20000元人民币，存期一年，年利率为1.98%，到期应交纳所利息的20%的利息税，那么到期取款并交利息税后，陈新的父亲可取回（ ）
A、20158.4元 B、20316.8元 C、20396元 D、20198元
3、现有以下四个结论:①绝对值等于其本身的有理数只有零;②相反数等于其本身的有理数只有零;③倒数等于其本身的有理数只有1; ④平方等于其本身的有理数只有1,其中正确的有( )
A、0个 B、1个 C、2个 D、3个
4、 –[a-(b-c)]去括号应为（ ）
A、-a+b+c B、 -a+b-c C、-a-b-c D、 -a-b+c
5、把27430按四舍五入取近似值,保留两位有数数字, 并用科学记数法表示的是( )
A、2.8×104 B、2.8×103 C、2.7×104 D、2.7×103
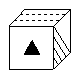
6、如图所示正方体,下列是其平面展开图的是( )
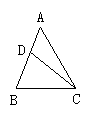
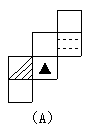
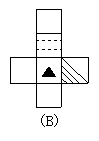
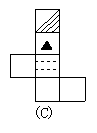
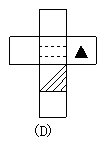
7、如图,共有线段的条数和角的个数分别是( )
A、5条,7个; B、5条,8个; C、6条,7个; D、6条,8个
8、为了解某校学生每日运动量,收集数据正确的是( )
A、调查该校七年级学生每日运动量； B、调查该校女生每日的运动量
C、调查该校男生每日的运动量；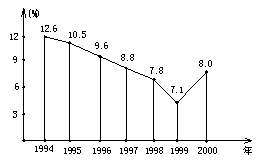
D、从七、八、九年级各抽调100人调查他们每日的运动量
9、近年来,国内生产总值增长率的变化情况如图,从上图看, 下列结论不正确的是( )
A、1995-1999年国内生产总值增长率逐年减少;
B、2000年国内生产总值的年增长率开始回升
C、这7年中,每年的国内生产总值不断增长;
D、这7年中,每年的国内生产总值有增有减
10、甲、乙两个药品仓库共存药品45吨，为共同抗击“禽流感”，现从甲仓库调出库存药品的60%，从乙仓库调出40%支援疫区，结果乙仓库所余药品比甲仓库所余药品多3吨，那么甲、乙两仓库原来所存药品分别为（ ）
A、24吨、21吨 B、21吨、24吨 C、25吨、20吨 D、20吨、25吨
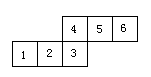
11、如图是正方体的平面展开图，每个面都标注了数字，如果2在正方体的左面，3在下面，那么正面的数字是（ ）
A. 1 B. 4 C. 5 D. 6
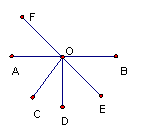12、如图，直线AB交EF于点O，已知∠AOD=∠COE=900，则下列结论 F
①∠AOC与∠ BOE互余；②∠ FOD=∠ BOC ③ ∠COD与∠ FOB互余
④∠ FOB-∠ DOE=900，其中正确的结论个是（ ）
A 1个 B 2个 C 3个 D 4个
三、计算（每小题5分，共10分）
1、 
2、-
×[-32×(-
)2-2];
四、解方程（每小题5分，共10分）
1、 2(x-2)-3(4x-1)=9(1-x).
2、
.
五、延长线段AB至C，使BC=2AB，如果线段AB=60cm，AB的中点是D，E，F两点在BC上，且BE∶ EF=1 ∶2，EF∶ FC=2∶ 5，求线段DF，FC的长？（5分）
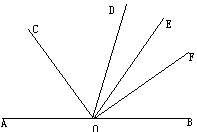六、如图，A、O、B在同一直线上，∠DOE=20º，OC平分∠AOD，OF平分∠EOB，求∠COF的度数。（5分）
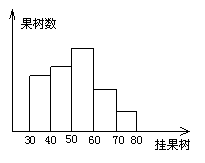
七、某果农承包了一片果林,为了了解整个果林的挂果情况, 果家随机抽查了部分果树挂果树进行分析.下图是根据这组数据绘制的统计图,图中从左到右各长方形之比为5:6:8:4:2,又知挂果数大于60的果树共有48棵.
(1)果农共抽查了多少棵果树?
(2)在抽查的果树中,挂果树在40-60之间的树有多少棵,占百分之几?（5分）
八、列方程解应用题（2题5分，其余每小题6分，共17分）
1、某车间共90名工人，每名工人平均每天加工甲种部件15个或乙种部件8个，问应安排加工甲种部件和乙种部件各多少人，才能在每天加工后使每3个甲种部件和2个乙种部件刚好配套？
2、一份稿件，若用人工抄写，3小时可以抄完，若用电脑打印，2小时可以完成，已知电脑打印每小时比人工抄写多200字，问这这稿件有多少字？
3、经过市场调查获取信息，生产一种绿色食品，若市场直接销售，每吨可获利润1000元，经粗加工后销售每吨利润可达4500元，经精加工后销售每吨利润可达7500元。一家食品公司加工生产能力是：如果进行粗加工，每天可加工16吨；如果进行精加工，每天可加工6吨，但两种加工方式不能同时进行，受季节影响，该公司共有140吨食品必须在15天加工销售完毕，为此公司研究了可行方案。
⑴将食品全部进行粗加工后销售，则可获利润_________元。
⑵将食品尽可能多的进行精加工，没来得及加工的在市场上直接销售，则可获利润______元。
你能为公司再设计第三种更好的方案，使公司比原来获取更多的利润吗？如果设计新的加工方案。请通过列方程的方法，求出可获取的最高利润。