初一数学试卷
（考试时间：120分钟 满分：100分）
| 题 号 | 一 | 二 | 三 | 四 | 五 | 总 分 | 评卷人 |
| 得 分 |
|
|
|
|
|
|
|
命题：曹康冕 审题： 审核：
一、填空题（每空1分，共30分）
1、同分母分数相加，分母不变，分子相加。这个运算法则可以用字母表示成 。
2、a的倒数与b的倒数的差，用代数式表示： 。
3、m，n的和除以m，n的差，用代数式表示： 。
4、若25xym-1和5mxy3m-7是同类项，则m= 。
5、用四舍五入法对下列各数按括号中的要求取近似值：
1）2.768≈ （精确到百分位） 2）8.965≈ （精确到0.1）
3）0.009403≈ （保留3位有效数字）
6、2–8= ； -( )
= 。
7、用科学计数法表示：
1）= （保留3位有效数字） 2）803400= 。
8、看数轴，用“<”或“>”填空： 0 a
b
1） 2a+6 2b+6 2）–3a–8 –3b–8
9、-x3y+3x2-7是 次 项式，其中最高次项的系数是 。
10、多项式x3y-x2y3-1-y2x，按x的升幂排列是 。
11、一元一次方程的标准式是 （其中a 0），它的解是
12、在3x+4y= 9中，如果2y = 6，那么x= 。
13、由2x–3y–4 = 0中，可以得到用x表示y的式子y= 。
14、如果x=5，y=7满足kx–2y = 1，那么k= 。
15、若2(m+3)2+2–n2=0，则(m + n)3= 。
16、当3<a<4时，则 a–3 + a–4= 。
17、一段路程长s千米，汽车需要a小时，步行需要b小时，步行比汽车每小时慢 千米。
18、( )5 = (8×8×8×8×8)(a •a •a •a •a)。
19、当n是奇数时，(–2a2)n= 。
20、8m×(–8)3×8m= ， 100•10m•10m+1= 。
二、选择题（每题2分，共10分）
21、与它的倒数相等的有理数是 （ ）
A、-1 B、0 C、1 D、±1
22、若x<0，则
等于
（ ）
A、1 B、0 C、-1 D、±1
23、下面几种说法正确的是 （ ）
A、若ac=bc， 则a=b
B、若 
，则a=b
C、若a2 = b2，则a=b D、若
，则x=-2
24、不等式10(x+4)+x≤84的整数解有 个。 （ ）
A、4 B、5 C、6 D、无数个
25、一个两位数，十位数字为a，并且十位数字比个位数字的一半还小1，那么这个两位数可以表示为 （ ）
A、10a+(2a+2) B、10a+(
-1) C、10a+(2a-2) D、10a+(+1)
三、解下列不等式、不等式组、方程或方程组（每题3分，共15分）
26、4(3x-1) < 5(2x+1)
27、 2x+7 < 3x-1
≥0
28、ax+b > 0
29、
30、 
6(x+y)=4(2x-y)+16
四、先化简在求值（每题3分，共15分）
31、3x2-[2x-2(2x-3)+7x2]，其中x=
。
32、(8x2+6x+1)(-8x2+6x-1)，其中x=。
33、(1-4y)(1+4y)+(1+4y)2，其中y=
。
34、8m2-5m(-m+3n)+4m(-4m-
n)，其中m=2，n=-1。
35、
，其中x=-1，y=-2
五、应用题（共30分）
36、班上组织同学们看电影，购买了甲、乙两种电影票共45张，甲种票5元/张，乙种票3元/张，共用去175元。求甲、乙两种电影票各买了多少张？（4分）
37、甲每天制造5个零件，乙每天制造7个零件，如果甲先做4天后乙才开始做，问乙做了几天后两人所做的零件数相同？（4分）
38、已知梯形的面积是42cm2，高是6cm，它的下底比上底的2倍少1cm。求梯形的上下底各是多少？（4分）
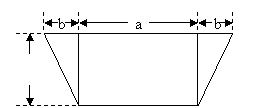
39、一条水渠，其横断面积为梯形。根据如图所示的长度求出横断面积S的代数式；计算当a=2，b=0.8时,梯形的面积是多少（5分）
  |
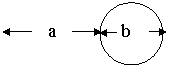
40、如图所示，一块直径为a+b的圆形钢板，从中挖去直径分别为a与b的两个圆。求剩下的钢板的面积S（用代数式表示）；若a=3，b=1，剩下的钢板的面积是多少？（5分）
 |
41、把一堆苹果分给几个孩子，如果每人分3个，则可剩余8个；如果前面每人分5个，则最后一个孩子得到的苹果不足3个，求小孩的人数和苹果的个数各是多少？（8分）