初一数学创新题B卷
一、填空题（每题2分，共30分）
1、地球的赤道半径约为米，用科学记数法表示为___________米，用四舍五入法保留三个有效数字取近似数为____________米。
2、月球表面的温度中午是101℃,半夜是－153℃，中午比半夜高______℃.
3、大于 -
而小于1
的整数是
.
4、已知∠α=128º18’，则它的补角为______度。
5、若
是同类项，则
。
6、若0<x<1,则把x, 
,
从小到大排列为： .
7、3个连续奇数中，n为最大的奇数，则这3个数的和为 .
8、代数式
的值为8，则代数式
的值为_________.
9、礼堂第一排有a个座位，后面每排都比第一排多1个座位，
则第n排座位有 个.
10、如图，有一多边形。这个多边形的周长是_________cm。
11、如图，已知∠AOB是直角，∠AOC是∠COB的3倍，则
∠COB是 度.
12、8箱苹果，以每箱5千克为准，称重记录如下（超过为正数）：
1.5 ， -1， 3 ， 0 ， 0.5 ， -1.5 ， 2 ， -0.5 。那么
8箱苹果的总重量是 千克。
13、已知a与b互为相反数，c与d互为倒数，m的绝对值为6，
则
的值为
.
14、已知M、N是线段AB上两点，且AB＝9，若点M是线段AB的
中点，MN＝
，则线段BN的长是 。
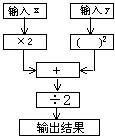
15、右图是一个数值转换机的示意图，若输入
的值为3，
的值为
时，则输出的结果为__________．
二、选择题（每题3分，共24分）
16、下列语句中，正确的是（ ）
A、0，
，1，2，3.2都是正数
B、0，—3，—2，—1都是负数
C、—1，0，1，2都是整数 D、—1，0，1，2都是自然数
17、下列各式中与a-b-c的值不相等的是（ ）.
A、a-(b+c) B、a-(b-c) C、(a-b)+(-c) D、(-c)+(a-b)
18、如果（
）的倒数是3，那么x的值是（ ）.
A、-3 B、1 C、3 D、-1
19、直线a、b、c中,a∥b,a∥c,则直线a与直线c的关系是（ ）.
A、相交 B、平行 C、垂直 D、不确定
20、下列说法正确的是（ ）.
A、两点之间的距离是两点间的线段
B、与同一条直线垂直的两条直线也垂直
C、同一平面内，过一点有且只有一条直线与已知直线垂直
D、同一平面内，过一点有且只有一条直线与已知直线平行
21、今年桔子的价格比去年提高了10%，如果今年的价格每千克a元，则去年的价格是每千克（ ）元.
A、(1+10%)a B、(1-10%)a C、
D、
22、下列说法中正确的是（ ）
A、可能性很大的事情是必然发生的 B、可能性很小的事情是不可能发生的
C、必然发生与不可能发生都是必然现象 D、可能发生的可能性没有大小之分
23、根据规律：
；则横线上应填的数为（ ）
B、
C、
D、
三、计算题(第（1）（2）每题各4分，第（3）题5分，共13分)
24、（1）
（2）用计算器计算:
(精确到0.1)
（3）化简求值: 
,其中x、y满足x-y+1+
=0.
四、画图题（共6分）
25、画出右图的三视图。
五、解答题(共27分)
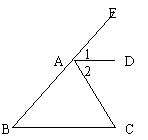26、已知：B、A、E在一条直线上，∠1=∠B,问：∠2与∠C相等吗？为什么？（4分）
27、小明调查了2004年12月15日这一天的气温变化情况，通常是每天调查四次，分别是2时、8时、14时、20时，结果如下表：(8分)
| 时间（时） | 2 | 8 | 14 | 20 |
| 温度（度） | 4 | 7 | 15 | 12 |
（1）请据此做出合适的统计图；
(2)请求出这一天的平均气温；
(3)从这些数据中你能得哪些信息，有如何感受.
28、张先生看到银行公布的存款利率如下表所示：
| 整存整取 | 一年 | 二年 | 三年 |
| 年利率(%) | 2.25 | 2.43 | 2.88 |
张先生要将一笔钱存入银行3年，它可以选择一次存3年，也可分几次存够3年，每次都将所有本息一笔存入，请你回答：(6分)
（1）有多少种获息不同的存取方式？
（2）在各种获息不同的存取方式中，哪种方案获息最高？请说明理由（暂不考虑利息税）。
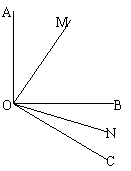
29、（1）如图，已知∠AOB=90º，∠BOC=30º，OM平分∠AOB，ON平分∠BOC，求∠MON的度数；(2分)
（2）如果（1）中∠AOB=α，∠BOC=β（β为锐角）,其他条件不变，求∠MON的度数；(2分)
（3）从（1）、（2）的结果中能得出什么结论？(2分)
（4）线段的计算与角的计算存在着紧密的联系，它们之间可以互相借鉴解法，请你模仿设计一道以线段为背景的计算题，并给出解答。(3分)
六、附加题
甲、乙、丙3人，甲每分钟行60米，乙每分钟行67.5米，丙每分钟行75米，如果甲乙二人在东村，丙在西村，他们3人同时由两村相向而行，丙遇到乙后，继续行走10分钟才遇到甲。东西两村相距多少米？