初一数学第二学期期终考试

初一数学第二学期期终考试

一、填空题：（每空1分，共21分）

1. 计算：

　　①a·a²·a³=_____________　　　　②(－2xy²)³=____________

③(－m⁵)⁴÷m¹²=___________　　　　④(2x－y)(y－2x)=______________

⑤()^－2+(3.14－π)⁰=_______　　 ⑥5.76²－4.24²=___________

2.0.000649用科学记数法表示为_____________；若(x+2)⁰有意义，则x______.

3.若一个角的邻补角比它的余角的3倍还少12°，则这个角是________度.

4.把命题“邻补角的角平分线互相垂直”改写成“如果……，那么……”的形式是：如果___________________________，那么___________________________.

5.已知：直线AB、CD相交于点O，OE平分∠BOD，若∠AOE=150°，则

1

∠AOC=_____°.　　　　　　　　　　　　　　　  c　d

2

　　　　 　　　　　　　　　　　　　　　　　　　　　　　　 a

　 C　　　　　　  B

4

　　　　　　　　  E

　　　　 O　　　　　　　　　　　　　　　 3　　　　　　　　　 b

　A　　　　　　　  D

　　　　第5题　　　　　　　　　　　　　　　　　第6题

6.已知：如图，直线a、b被c、d所截，∠1=110°，∠2=125°，∠3=70°，

则∠4=_____°.

7.如图，ΔABC中，∠BAC的平分线交BC于点E，在AE的延长线上取一点F，作

　FD⊥BC于点D，已知∠B=64°，∠C=22°，则∠F的度数为_______°.

A

C

　　　　　  F

　　　　　　　　　　　　　　　　　　　　　　　　 A　　　　　 D

O

D

　　　

　　　　  E　　　　　　　　　　　　　　　　　　　　 

　　A　　　　 B　　 B　　　D　 E　　 C　　　　 B　　　　　　　 C

　　　　第7题　　　　　　 第8题　　　　　　　　　  第9题

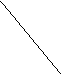
8.如图，已知ΔABE≌ΔACD，∠B=∠C，∠AEB=∠ADC，AB的对应边是______，

　 另一组对应角是______________________.

9.已知，如图，∠ACB=∠DBC，要使ΔABC≌ΔDCB，必须增加一个条件是

___________________________(只需填一个你认为合适的条件).

10.若m²+n²+2m－6n+10=0，则n^m=_________.

11.化简：(a―4b+3c)(a+4b―3c)=____________________________.

12.若ΔABC的三边长都是整数，周长为11，且有一边长为4，则这个三角形可能 的最大边长是___________.

13.已知a、b、c是ΔABC的三边长，且a²－ab+bc－c²=0，则ΔABC的形状是

　 _________________________.

二、选择题（每题2分，共20分）

14.已知一个等腰三角形的两边长分别是4和8，则它的周长是（　　）

　 A．20　　　　B.16　　　　C.20或16　　　 D. 12或16

15.下列多项式能分解成(x―6)(x+1)的是（　　）

A.x²+5x+6　　B.x²+5x―6　 C.x²―5x+6　　 D.x²―5x―6

16. 下列各式中不能用完全平方公式分解的是（　　）

A.―x²+2xy―y²　 B.x⁴―2x³y+x²y²　 C. m²―m+1　　D、x²―xy+y²

17.在ΔABC中，若∠A+∠C=∠B，则ΔABC一定是（　　）

A.等腰三角形　　　　B.锐角三角形　　C.直角三角形　 D.钝角三角形

18.下列式子变形错误的是（　　）

A.15a²+5a=5a(3a+1)　　　　　B. ―x²―y²=―(x+y)(x―y)

北

C.ax+x+ay+y=(a+1)(x+y)　　　D.a²―bc-ab+ac=(a―b)(a+c)

19.在甲、乙两地修一条笔直的公路，从甲地

测得公路走向是北偏东36°，甲、乙两　　  　　　 

地同时开工，要使若干天后公路准确接　　　　　　　  乙

通，乙地所修的公路走向是（　　）　　　　 北　　　　　 

东

西

A.北偏东36°　　B.南偏西36°　　　　　　

C.北偏东54°　　D、南偏东54°　　　　　  甲

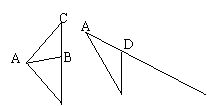
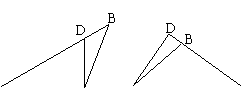
20、画ΔABC中BC边上的高，在下图的画法中，正确的是（　　 ）

D

C

C

C

B

A

A

　　

　 　　　　　　　　　　　　　　　　　　　　　　　　　 

E

F

A

21.已知：如图，AB=AC，AD平分∠BAC，点0在

AD上，BE、CE经过点O并分别交AC、AB于

点E、F，图中共有全等三角形的对数是

O

C

（　 ）　　　　　　　　　　　　　　　

B

A.4对　 B.5对　　C.6对　　D.7对　　　　　　　　　

	D

22.下列四个条件，可以判定ΔABC和ΔDEF全等的是（　　）

　　A、BC=EF，AC=DF，∠B=∠E　　B、AB=AC，DE=DF，∠A=∠D

C、AC=DF，∠A=∠D，∠B=∠E　D、∠A=∠D，∠B=∠E，∠C=∠F

23.下列命题中真命题的个数是（　　）

　　①有两条边和其中一边上的中线对应相等的两个三角形全等

②全等三角形对应角的平分线相等

③有两边和其中一边的对角对应相等的两个三角形全等

④有两角和其中一角的对边对应相等的两个三角形全等

A、1个　　　B、2个　　　C、3个　　　D、4个

三、解答题：

24.计算（每题3分，共9分）

(1)(―4xy³)·(x²y―xy²―y³)　　　　(2)(x+1)(x²―2x)(x―1)

(3)(27a³b⁵―6a²b⁴+15a⁴b³)÷(―3a²b³)

25.化简求值：（4分）

　a³·（3a―2）―a（3a—2）² + 6a（2—3a）,其中a=4

26.把下列各式因式分解：（第<1>,<2>,<3>题各3分，第4题4分，第5题5分）

　(1)x²y―2xy+y　　　　　　　　 (2)16m²―(2m―3n)²

(3)(x²+3x)²―3(x²+3x)―4　　　 (4)(a+b)(a―b)+4(b－1)

(5)x³(x―2y)+y³(2x―y)

27.（4分）如图，AB∥CD，EF交AB于E，　　　　　　　　　 E

交CD于F，若∠AEF=68°，FN平分　　　　　  A　　　　　　　 B

∠EFD， NG∥AB，　　　　　　　　　　  　　　　　　　 N　　　 G

F

求∠FNG的度数。　　　　　　　　　　　　　 C　　　　　　　　 D

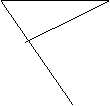
28.（5分）已知：如图，AE∥DF，AE=DF，AC=DB，求证：BE=CF且BE∥CF

　　A　　　　　　  E

C

　　　　B

　　　　　　　

F

　　　　 

　　　　　　　 D

　　　

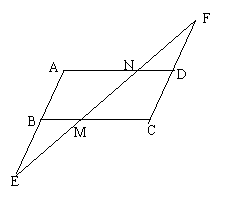
29、（6分）已知，如图，AD=BC，AB=CD，分别延长AB、CD到E、F，使BE=DF，

连结EF，分别交BC、AD于M、N

(1)求证：∠E=∠F

(2)若BC=8，ND=3，求MC的长.

30.（6分）求证：如果两个三角形有两个角和其中一个角对边上的高对应相等，那么这两个三角形全等。

31.（7分）已知：在ΔABC中，∠ACB=90⁰，CE⊥AB，垂足为E，AF平分∠CAB交BC于点F，点D在AB上，且AD=AC.

(1)　求证：∠ECB=∠DFB.

(2)若AF与CE交于点O，连结OD，求证：OD∥BC.

　 A

E

　　　　

D

O

　　　　　　

附加题（10分×2=20分）

1.若x²―24y²+3x+34y―10xy+k可分解成两个系数为有理数的一次因式的乘积形式，求k的值，并将这个多项式因式分解。

2.如图，AH是ΔABC中BC边上的高，AB⊥AD于A，AC⊥AE于A，AB=AD，

　AC=AE，HA的延长线交DE于点M，求证：点M是DE的中点。

 

D　　　　 M

　　　　　　　　　　E

　　　　A

	B				C
			H

命题：初一备课组　校对：吴新元

责审：马美君　　　审定：教务处