初一数学期末复习提纲
班级 姓名 号数
一、选择题：
1．方程
的解是
（ ）
（A）
（B）
（C）
（D）
2.不等式组
的解集在数轴上表示,正确的是( )
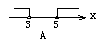
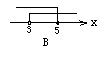
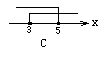
3.以下列各数为边，能组成三角形的是＿＿＿＿＿。
A、2，2，5 B、4，7，3 C、5，2，8 D、11，9，6
4．解为
的方程组是
（ ）
（A）、
（B）、
（C）、
（D）、
5.下列不一定是轴对称图形的是＿＿＿＿。
A、等腰三角形 B、正方形 C、圆 D、三角形
6.某商店出售下列形状的地转：①正方形②长方形③正五边形④正六边形⑤正三角形，若只选购其中某一种地转镶嵌地面，可供选择的地转共有（ ）
A．1种 B．2种C．3种D．4种
7.在开山工程爆破时，已知导火索燃烧速度为0.5cm／s，人跑开的速度为4m／s，为了使点燃导火索的同志在爆破时能跑到100 m以外的安全区，设导火索的长度x cm，应满足的不等式为（ ）。
A、4×
≥100 B、4×≤100 C、4×＞100 D、4×＜100
二、填空题：
1.一元一次方程x－5＝7的解x＝ ；
2.由x＋2 y = 5，得到用y表示x的式子为x = ；
3. 不等式
x＞4的解集是
，
不等式
非负整数解是
，
4.用不等式表示： x的2倍与4的差是正数 ；
x的绝对值与1的和不小于1 。
5．当x＝ 时，代数式2x+3与3－5x的值互为相反数。
6.方程组
的解是
。
7．方程
的解是
.
8.若x＝1是关于x的方程3 x－2 m＝5的解，则m = ；
9.不等式组2≤3x－7<8的整数解为_________________________；
10．如果
是方程组
的解，则a＝＿＿＿，b＝＿＿＿＿。
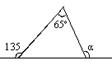
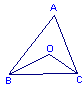11．如图所示，∠α =___度.
12．已知三角形的两边长分别为3和5，
则第三边长a的范围是
13.如图，△ABC中，∠ABC和∠ACB的平分线交于点O，
若∠BOC=110°, 则∠A=______°
14.十边形的内角和是 度。
15．一个多边形的每一个外角都是30°，那么这个多边形的边数为 。
16．等腰三角形两边长分别是5cm 和8cm，则其周长是 .
17．等腰三角形的一个角为50°，它的另外两个角的度数为＿＿＿＿
18．等腰三角形有两个内角的度数比为4：1，则顶角的度数是
。
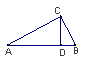
19．如图，在ΔABC中，∠ACB＝90°，CD⊥AB于D，
若∠BCD＝30°，则∠A＝＿＿度。
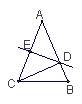
20．如图3，
中，DE是AC的垂直平分线，AC＝6cm，
的周长为13cm。则的周长是＿＿＿＿＿＿＿
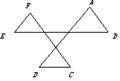
21．如图，∠A+∠B+∠C+∠D+∠E+∠F=
22．已知梯形的上底a＝3，高h＝5，面积S＝20，
根据梯形的面积公式S＝
（a+b）h，则下底b的长为 ；
23．国家规定：存款利息税 = 利息×20%，银行一年定期储蓄的年利率为1.98%。小明有一笔一年期存款，如果到期后全取出，可取回1219元。若小明的这笔存款是x元，根据题意，可列方程为 。
24．若ΔABC边为a、b、c，则a－b－c＋b－c－a＋c－a－b＝＿＿＿。
三、解答题：
1．
（写检验）
2．
（画数轴）
3．
4． 
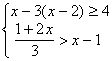
5．在等式
中，当x＝1时，y＝－2；当x＝－1时，y＝－4.求k、b的值。
6．已知方程组
的解x为非正数，y为负数，求
的取值范围。
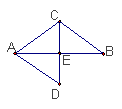7．如图，已知线段CD垂直平分AB，AB平分
，问AD与BC平行吗？请说明理由。
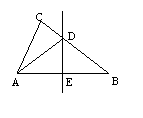
8．如图，△ABC中，ÐC=90°，DE为斜边AB的垂直平分线，ÐDAE与ÐDAC的度数的比为2∶1；求ÐB的度数．
9．甲、乙两人各自抛掷一个普通的正方体骰子，如果两者之积为奇数，那么甲得1分；如果两者之积为偶数，那么乙得1分。连续抛掷20次，谁得分高，谁就获胜。
①请你想一想，谁获胜的可能性大？为什么？
②你认为这个游戏公平吗？如果不公平，请你设计一个公平的游戏规则。
10．世界杯决赛分成八个小组，每小组4个队，小组进行单循环（每个队都与该小组的其他队比赛一场）比赛，选出2个队进入16强，胜一场得3分，平一场得1分，负一场得0分。请问：①每小组共比赛多少场？
②在小组比赛中，现有一队得到6分，该队出线是一个确定事件，还是不确定事件？（本题8分）
11.厦门火车货运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货运往广州,这列货车应挂A、B两种不同规格的货厢50节.已知甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,有几种运输方案?请你设计出来.